pacman::p_load(olsrr, corrplot, ggpubr, sf, spdep, GWmodel, tmap, tidyverse, gtsummary, httr, onemapsgapi, jsonlite, units, matrixStats, rvest, SpatialML, Metrics)Take-Home Exercise 3: Predicting HDB Public Housing Resale Pricies using Geographically Weighted Methods
Introduction
Background and Objective
Housing plays a vital part in our day-to-day lives, and purchasing a home is a significant investment for most people. The cost of housing is influenced by various factors, including global economic conditions and property-specific variables such as its size, fittings, and location.
In this exercise, we will be examining the relationship between HDB Resale Flat Prices and some of these factors, such as the location and age of the resale flat, and proximity to amenities.
Defining the Study Period
For this study, we will be examining a 2-year period of Resale Flat Prices, between Jan 2021 and Dec 2022. We will then conduct geographically weighted regression, and use the months of Jan and Feb of 2023 to test our model.
Data Set Selection
For this exercise, we will be using the below data sets:
Geospatial
- Singapore Master Plan 2019 Subzone Boundary
- Location of Eldercare Centres (from data.gov.sg)
- Location of Hawker Centres (from data.gov.sg)
- Location of MRT Exits (from LTA Data Mall)
- Location of Parks (from data.gov.sg)
- Location of Supermarkets (from data.gov.sg)
- Location of Kindergartens (from data.gov.sg)
- Location of Childcare (from data.gov.sg)
- Location of Bus Stops (from LTA Data Mall)
Aspatial
- HDB Resale Flat Prices (from data.gov.sg)
- Primary Schools as of 2017 (from data.world)
Others
Best Primary Schools 2021 (from salary.sg)
Mall Coordinates WebScraper (from https://github.com/ValaryLim/Mall-Coordinates-Web-Scraper)
Imports
Let us start with importing all the appropriate packages and data sets.
Import Packages
Import Geospatial Data
Singapore Master Plan 2019 Subzone Boundary Dataset
mpsz = st_read(dsn = "data/geospatial/MPSZ-2019", layer = "MPSZ-2019")Reading layer `MPSZ-2019' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/MPSZ-2019'
using driver `ESRI Shapefile'
Simple feature collection with 332 features and 6 fields
Geometry type: MULTIPOLYGON
Dimension: XY, XYZ
Bounding box: xmin: 2667.538 ymin: 15748.72 xmax: 56396.44 ymax: 50256.33
z_range: zmin: 0 zmax: 0
Projected CRS: SVY21 / Singapore TMst_crs(mpsz)Coordinate Reference System:
User input: SVY21 / Singapore TM
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Elder Care Centers Data Set
eldercare = st_read(dsn = "data/geospatial/Eldercare", layer = "ELDERCARE")Reading layer `ELDERCARE' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/Eldercare'
using driver `ESRI Shapefile'
Simple feature collection with 133 features and 18 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 14481.92 ymin: 28218.43 xmax: 41665.14 ymax: 46804.9
Projected CRS: SVY21eldercare <- st_transform(eldercare, 3414)st_crs(eldercare)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Hawker Centers Data Set
hawker_centre = st_read(dsn = "data/geospatial/HawkerCentres/hawker-centres.geojson")Reading layer `hawker-centres' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/HawkerCentres/hawker-centres.geojson'
using driver `GeoJSON'
Simple feature collection with 125 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6974 ymin: 1.272716 xmax: 103.9882 ymax: 1.449217
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84hawker_centre <- st_transform(hawker_centre, 3414)st_crs(hawker_centre)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]MRT Data Set
mrt_exit = st_read(dsn = "data/geospatial/TrainStationExit", layer = "Train_Station_Exit_Layer")Reading layer `Train_Station_Exit_Layer' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/TrainStationExit'
using driver `ESRI Shapefile'
Simple feature collection with 562 features and 2 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 6134.086 ymin: 27499.7 xmax: 45356.36 ymax: 47865.92
Projected CRS: SVY21mrt_exit <- st_transform(mrt_exit, 3414)st_crs(mrt_exit)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Parks Data Set
parks = st_read(dsn = "data/geospatial/Parks/parks.kml")Reading layer `NATIONALPARKS_New' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/Parks/parks.kml'
using driver `KML'
Simple feature collection with 421 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6929 ymin: 1.214491 xmax: 104.0538 ymax: 1.462094
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84parks <- st_transform(parks, 3414)st_crs(parks)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Supermarkets Data Set
supermarkets = st_read(dsn = "data/geospatial/supermarkets.kml")Reading layer `SUPERMARKETS' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/supermarkets.kml'
using driver `KML'
Simple feature collection with 526 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6258 ymin: 1.24715 xmax: 104.0036 ymax: 1.461526
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84supermarkets <- st_transform(supermarkets, 3414)st_crs(supermarkets)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Kindergartens Data Set
kindergartens = st_read(dsn = "data/geospatial/kindergartens.kml")Reading layer `KINDERGARTENS' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/kindergartens.kml'
using driver `KML'
Simple feature collection with 448 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6887 ymin: 1.247759 xmax: 103.9752 ymax: 1.455452
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84kindergartens <- st_transform(kindergartens, 3414)
st_crs(kindergartens)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Childcare Centers Data Set
childcare = st_read(dsn = "data/geospatial/childcare.geojson")Reading layer `childcare' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/childcare.geojson'
using driver `GeoJSON'
Simple feature collection with 1545 features and 2 fields
Geometry type: POINT
Dimension: XYZ
Bounding box: xmin: 103.6824 ymin: 1.248403 xmax: 103.9897 ymax: 1.462134
z_range: zmin: 0 zmax: 0
Geodetic CRS: WGS 84childcare <- st_transform(childcare, 3414)
st_crs(childcare)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Bus Stops Data Set
bus_stops = st_read(dsn = "data/geospatial/BusStop_Feb2023", layer = "BusStop")Reading layer `BusStop' from data source
`/Users/michelle/Desktop/IS415/shelle-mim/IS415-GAA/Take-home_Exercise/TH3/data/geospatial/BusStop_Feb2023'
using driver `ESRI Shapefile'
Simple feature collection with 5159 features and 3 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 3970.122 ymin: 26482.1 xmax: 48284.56 ymax: 52983.82
Projected CRS: SVY21bus_stops <- st_transform(bus_stops, 3414)
st_crs(bus_stops)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Import Aspatial Data
HDB Resale Flat Prices
resale_prices_2017_onwards = read_csv("data/aspatial/resale-flat-prices-based-on-registration-date-from-jan-2017-onwards.csv")Now, we can separate out our data by date into our training and testing data.
resale_prices_2021_22 <- resale_prices_2017_onwards %>%
filter(month < '2023-01') %>%
filter(month > '2020-12')resale_prices_2023 <- resale_prices_2017_onwards %>%
filter(month < '2023-03') %>%
filter(month > '2022-12')Shopping Malls Data Set
malls = read_csv("data/aspatial/mall_coordinates_updated.csv")glimpse(malls)Rows: 184
Columns: 4
$ ...1 <dbl> 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17…
$ latitude <dbl> 1.274588, 1.305087, 1.301385, 1.312025, 1.334042, 1.437131, …
$ longitude <dbl> 103.8435, 103.9051, 103.8377, 103.7650, 103.8510, 103.7953, …
$ name <chr> "100 AM", "112 KATONG", "313@SOMERSET", "321 CLEMENTI", "600…malls <- st_as_sf(malls,
coords = c("longitude", "latitude"),
crs=4326) %>%
st_transform(crs = 3414)tmap_mode("plot")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(malls)+
tm_dots()
Primary Schools Data Set
pri_schs = read_csv("data/aspatial/primaryschoolsg.csv")glimpse(pri_schs)Rows: 190
Columns: 9
$ Name <chr> "Admiralty Primary School", "Ahmad Ibrahim Pr…
$ Type <chr> "Government", "Government", "Government-aided…
$ GenderMix <chr> "Mixed", "Mixed", "Mixed", "Mixed", "Mixed", …
$ Area <chr> "Woodlands", "Yishun", "Bishan", "Bukit Merah…
$ Zone <chr> "North", "North", "South", "South", "North", …
$ PostalCode <dbl> 738907, 768643, 579646, 159016, 544969, 56978…
$ Latitude <dbl> 1.4427, 1.4333, 1.3603, 1.2913, 1.3913, 1.383…
$ Longitude <dbl> 103.7995, 103.8321, 103.8321, 103.8233, 103.8…
$ PlacestakenuptillPhase2B <dbl> 130, 51, 302, 82, 101, 166, 211, 190, 29, 57,…pri_schs <- pri_schs %>% dplyr::select(c(0:1, 7:8))pri_schs <- st_as_sf(pri_schs,
coords = c("Longitude", "Latitude"),
crs=4326) %>%
st_transform(crs = 3414)tmap_mode("plot")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(pri_schs)+
tm_dots()
Data Wrangling
Now that we have imported all our data, we can start the data cleaning and transformation process in order to prepare our data for the predictive models we plan to run for it.
Core DataSet: HDB Resale Flat Prices
Firstly, if we look into our darta set, we see that the dataset only provides us the street name and block of the resale flats. In order to turn this into geospatial data, we will need the longitude and latitude of the each flat.
We will be using OneMapSgAPI in order to do this. Let us first write a function that will invoke the API for us and retrieve the longitude and latitude data we need.
geocode <- function(block, streetname) {
base_url <- "https://developers.onemap.sg/commonapi/search"
address <- paste(block, streetname, sep = " ")
query <- list("searchVal" = address,
"returnGeom" = "Y",
"getAddrDetails" = "N",
"pageNum" = "1")
res <- GET(base_url, query = query)
restext<-content(res, as="text")
output <- fromJSON(restext) %>%
as.data.frame %>%
select(results.LATITUDE, results.LONGITUDE)
return(output)
}Now, we can run this function on our datasets in order to populate the dataset. This code takes a long time to load, and as such is saved into and loaded from RDS.
# resale_prices_2021_22$LATITUDE <- 0
# resale_prices_2021_22$LONGITUDE <- 0
#
# for (i in 1:nrow(resale_prices_2021_22)){
# temp_output <- geocode(resale_prices_2021_22[i, 4], resale_prices_2021_22[i, 5])
#
# resale_prices_2021_22$LATITUDE[i] <- temp_output$results.LATITUDE
# resale_prices_2021_22$LONGITUDE[i] <- temp_output$results.LONGITUDE
# }
# resale_prices_2023$LATITUDE <- 0
# resale_prices_2023$LONGITUDE <- 0
#
# for (i in 1:nrow(resale_prices_2023)){
# temp_output <- geocode(resale_prices_2023[i, 4], resale_prices_2023[i, 5])
#
# resale_prices_2023$LATITUDE[i] <- temp_output$results.LATITUDE
# resale_prices_2023$LONGITUDE[i] <- temp_output$results.LONGITUDE
# }We can then do some null checks in order to make sure that our function properly populated our dataframe.
# sum(is.na(resale_prices_2021_22$LATITUDE))
# sum(is.na(resale_prices_2021_22$LONGITUDE))
# sum(resale_prices_2021_22$LATITUDE == 0)
# sum(resale_prices_2021_22$LONGITUDE == 0)# sum(is.na(resale_prices_2023$LATITUDE))
# sum(is.na(resale_prices_2023$LONGITUDE))
# sum(resale_prices_2023$LATITUDE == 0)
# sum(resale_prices_2023$LONGITUDE == 0)# # st_as_sf outputs a simple features data frame
# resale_prices_2021_22_sf <- st_as_sf(resale_prices_2021_22,
# coords = c("LONGITUDE",
# "LATITUDE"),
# # the geographical features are in longitude & latitude, in decimals
# # as such, WGS84 is the most appropriate coordinates system
# crs=4326) %>%
# #afterwards, we transform it to SVY21, our desired CRS
# st_transform(crs = 3414)
# # st_as_sf outputs a simple features data frame
# resale_prices_2023_sf <- st_as_sf(resale_prices_2023,
# coords = c("LONGITUDE",
# "LATITUDE"),
# # the geographical features are in longitude & latitude, in decimals
# # as such, WGS84 is the most appropriate coordinates system
# crs=4326) %>%
# #afterwards, we transform it to SVY21, our desired CRS
# st_transform(crs = 3414)In order to preserve this data, we will now save it to rds.
# saveRDS(resale_prices_2021_22_sf, file="data/rds/resale_prices_2021_22_sf.rds")
# saveRDS(resale_prices_2023_sf, file="data/rds/resale_prices_2023_sf.rds")And now we can load it.
resale_prices_2021_22_sf <- read_rds("data/rds/resale_prices_2021_22_sf.rds")
resale_prices_2023_sf <- read_rds("data/rds/resale_prices_2023_sf.rds")We can now display our data on the map.
tmap_mode("plot")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(resale_prices_2021_22_sf)+
tm_dots(col = "resale_price",
size = 0.01,
border.col = "black",
border.lwd = 0.5) +
tmap_options(check.and.fix = TRUE) +
tm_view(set.zoom.limits = c(11, 16)) +
tm_layout(legend.outside = TRUE)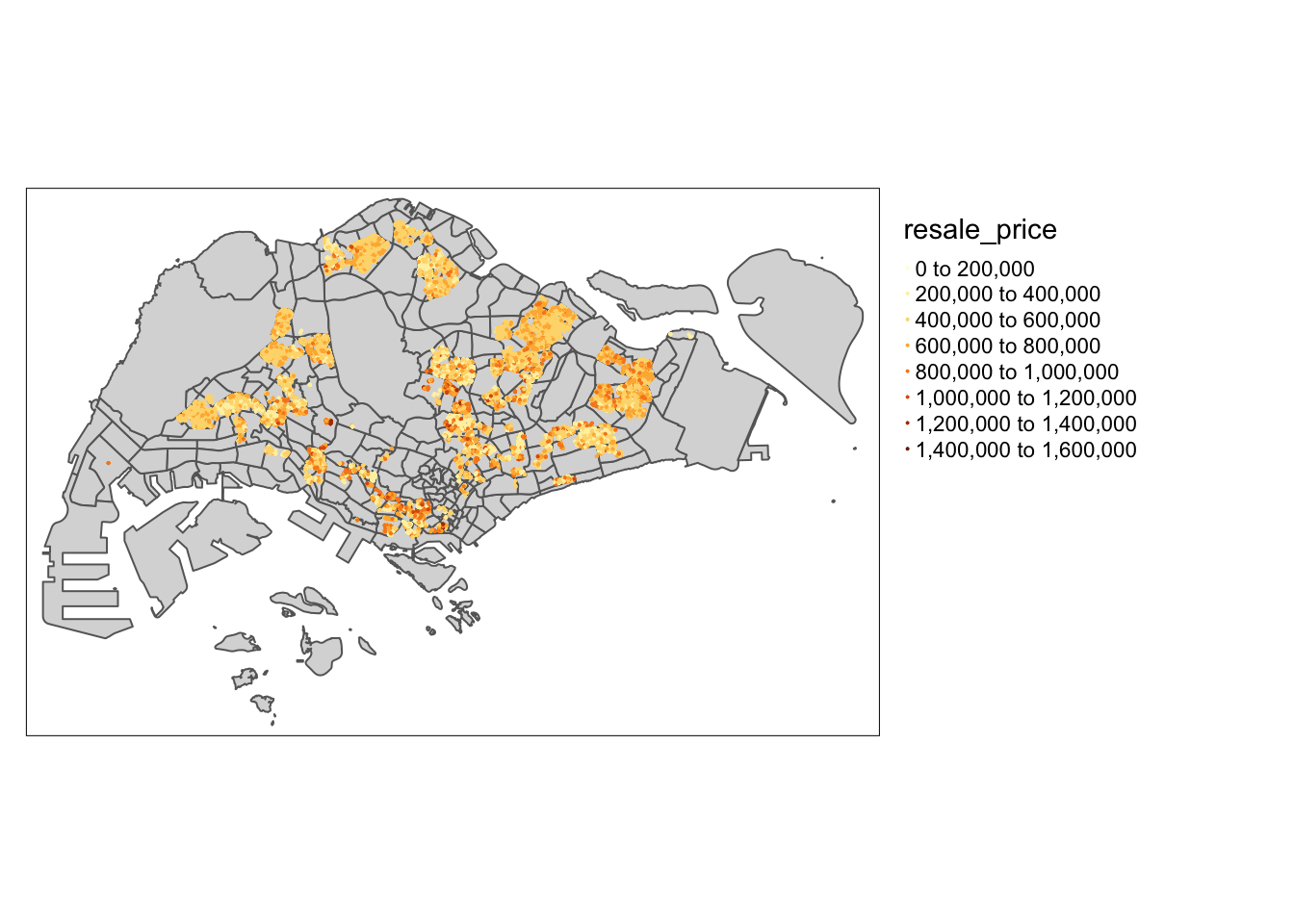
tmap_mode("plot")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(resale_prices_2023_sf)+
tm_dots(col = "resale_price",
size = 0.01,
border.col = "black",
border.lwd = 0.5) +
tmap_options(check.and.fix = TRUE) +
tm_view(set.zoom.limits = c(11, 16)) +
tm_layout(legend.outside = TRUE)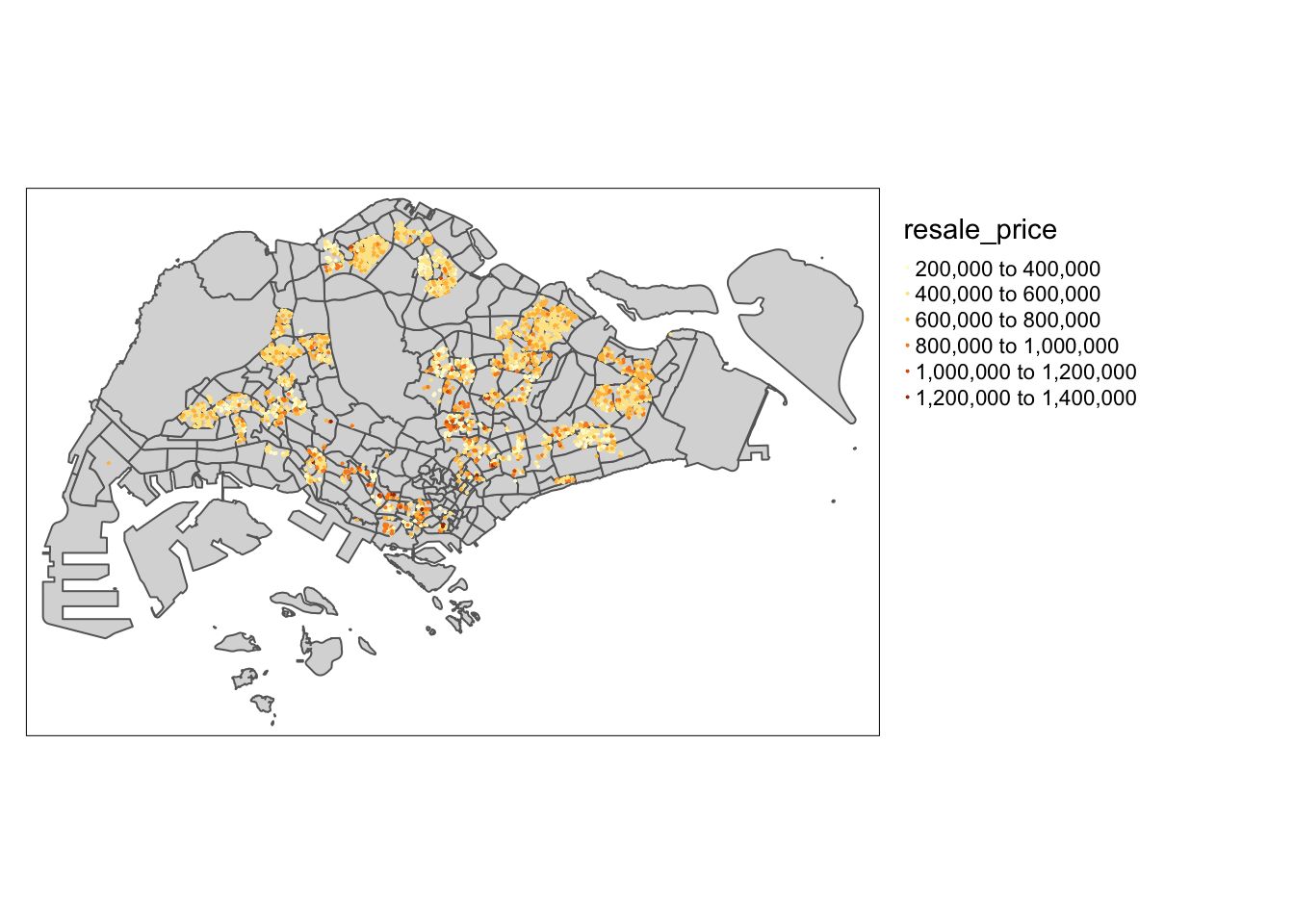
Geospatial Data
Now that we have transformed our HDB Resale Price data, we can move on to creating some of the other metrics we want to look at in our analysis.
Proximity to CBD
In order to get the distance to the CBD, we must first identify where the CBD is, then find its centre. We can then calculate the distance. Let us start by looking at the Planning Areas in our dataset.
unique(mpsz$PLN_AREA_N) [1] "MARINA EAST" "RIVER VALLEY"
[3] "SINGAPORE RIVER" "WESTERN ISLANDS"
[5] "MUSEUM" "MARINE PARADE"
[7] "SOUTHERN ISLANDS" "BUKIT MERAH"
[9] "DOWNTOWN CORE" "STRAITS VIEW"
[11] "QUEENSTOWN" "OUTRAM"
[13] "MARINA SOUTH" "ROCHOR"
[15] "KALLANG" "TANGLIN"
[17] "NEWTON" "CLEMENTI"
[19] "BEDOK" "PIONEER"
[21] "JURONG EAST" "ORCHARD"
[23] "GEYLANG" "BOON LAY"
[25] "BUKIT TIMAH" "NOVENA"
[27] "TOA PAYOH" "TUAS"
[29] "JURONG WEST" "SERANGOON"
[31] "BISHAN" "TAMPINES"
[33] "BUKIT BATOK" "HOUGANG"
[35] "CHANGI BAY" "PAYA LEBAR"
[37] "ANG MO KIO" "PASIR RIS"
[39] "BUKIT PANJANG" "TENGAH"
[41] "SELETAR" "SUNGEI KADUT"
[43] "YISHUN" "MANDAI"
[45] "PUNGGOL" "CHOA CHU KANG"
[47] "SENGKANG" "CHANGI"
[49] "CENTRAL WATER CATCHMENT" "SEMBAWANG"
[51] "WESTERN WATER CATCHMENT" "WOODLANDS"
[53] "NORTH-EASTERN ISLANDS" "SIMPANG"
[55] "LIM CHU KANG" As we can see, we already have the Downtown Core as a Planning Area. And as said by the Urban Redevelopment Authority, “The Downtown Core Planning Area is the economic and cultural heart of Singapore”, and encompasses the Central Business District. As such, we will be using the centroid of the
# Extract Downtown core
downtown_core <- mpsz %>%
filter(PLN_AREA_N == "DOWNTOWN CORE") %>%
st_combine()# Get Centroid
downtown_core_centroid <- downtown_core %>%
st_centroid()
downtown_core_centroidGeometry set for 1 feature
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 30468.27 ymin: 29912.14 xmax: 30468.27 ymax: 29912.14
Projected CRS: SVY21 / Singapore TM# Plot
tmap_mode("plot")
tm_shape(mpsz) +
tm_polygons() +
tmap_options(check.and.fix = TRUE) +
tm_shape(downtown_core) +
tm_fill(col = "pink") +
tm_shape(downtown_core_centroid) +
tm_dots() +
tm_view(set.zoom.limits = c(11, 16))
Great! We now have our centroid that we can use to calculate the distance to. We can now use the coordinates of our centroid and makew an sf dataframe for later use.
st_coordinates(downtown_core_centroid) X Y
[1,] 30468.27 29912.14lat <- 30335.19
lng <- 129721.45
downtown_core_centroid_sf <- data.frame(lat, lng) %>%
st_as_sf(coords = c("lng", "lat"), crs=3414)With that done, we can now calculate the Proximity to CBD. But before we do that, we need to change our centroid into an sf dataframe for comparison. We will do this altogether for all the seperate data sets in a later section for simplicity and data consistency.
Proximity to Good Primary School
For this metric, there were no readily available data sets. As such, we will attain this information via webscraping. We will be scraping https://www.salary.sg/2021/best-primary-schools-2021-by-popularity/, which provides a ranking of the Best Primary Schools by popularity.
url <- "https://www.salary.sg/2021/best-primary-schools-2021-by-popularity/"
good_pri <- data.frame()
schools <- read_html(url) %>%
html_nodes(xpath = paste('//*[@id="post-3068"]/div[3]/div/div/ol/li') ) %>%
html_text()
for (i in (schools)){
sch_name <- toupper(gsub(" – .*","",i))
sch_name <- gsub("\\(PRIMARY SECTION)","",sch_name)
sch_name <- trimws(sch_name)
new_row <- data.frame(pri_sch_name=sch_name)
# Add the row
good_pri <- rbind(good_pri, new_row)
}Since we are looking out for good primary schools, let us select the first 20 results that we will find the proximity to for our analysis.
top_pri_sch <- head(good_pri, 20)Since we already have the coordinates from our primary school data, we can left_join in order to add the coordinates to our list of top primary schools. But first, we need to do a little data preparation to make sure the columns match.
top_pri_sch$pri_sch_name[!tolower(top_pri_sch$pri_sch_name) %in% tolower(pri_schs$Name)][1] "CHIJ ST. NICHOLAS GIRLS’ SCHOOL" "CATHOLIC HIGH SCHOOL"
[3] "ST. HILDA’S PRIMARY SCHOOL" "HOLY INNOCENTS’ PRIMARY SCHOOL"
[5] "METHODIST GIRLS’ SCHOOL (PRIMARY)"It seems the issue lies with different apostrophes being used, as well as Catholic High School. We can easily change those to match our primary school dataset.
top_pri_sch$pri_sch_name <- gsub('’', "'", top_pri_sch$pri_sch_name)
top_pri_sch$pri_sch_name[top_pri_sch$pri_sch_name == 'CATHOLIC HIGH SCHOOL'] <- 'CATHOLIC HIGH SCHOOL (PRIMARY)'Now that that is settled, we can join the data to get out coordinates.
# Convert to lowercase for easy comparison
top_pri_sch$pri_sch_name <- tolower(top_pri_sch$pri_sch_name)
# Function to do our join for us
join_lowercase_name <- function(left,right){
right$Name <- tolower(right$Name)
inner_join(left,right,by=c("pri_sch_name" = "Name"))
}
top_pri_sch <- join_lowercase_name(top_pri_sch, pri_schs) top_pri_sch <- st_as_sf(top_pri_sch, crs=3414)
st_crs(top_pri_sch)Coordinate Reference System:
User input: EPSG:3414
wkt:
PROJCRS["SVY21 / Singapore TM",
BASEGEOGCRS["SVY21",
DATUM["SVY21",
ELLIPSOID["WGS 84",6378137,298.257223563,
LENGTHUNIT["metre",1]]],
PRIMEM["Greenwich",0,
ANGLEUNIT["degree",0.0174532925199433]],
ID["EPSG",4757]],
CONVERSION["Singapore Transverse Mercator",
METHOD["Transverse Mercator",
ID["EPSG",9807]],
PARAMETER["Latitude of natural origin",1.36666666666667,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8801]],
PARAMETER["Longitude of natural origin",103.833333333333,
ANGLEUNIT["degree",0.0174532925199433],
ID["EPSG",8802]],
PARAMETER["Scale factor at natural origin",1,
SCALEUNIT["unity",1],
ID["EPSG",8805]],
PARAMETER["False easting",28001.642,
LENGTHUNIT["metre",1],
ID["EPSG",8806]],
PARAMETER["False northing",38744.572,
LENGTHUNIT["metre",1],
ID["EPSG",8807]]],
CS[Cartesian,2],
AXIS["northing (N)",north,
ORDER[1],
LENGTHUNIT["metre",1]],
AXIS["easting (E)",east,
ORDER[2],
LENGTHUNIT["metre",1]],
USAGE[
SCOPE["Cadastre, engineering survey, topographic mapping."],
AREA["Singapore - onshore and offshore."],
BBOX[1.13,103.59,1.47,104.07]],
ID["EPSG",3414]]Proximity and Frequency Calculations
With all our data prepared and ready for use, we can now move on to calculations.
Let us now write functions to calculate the proximity and frequency of the relevant features to our resale price data:
proximity <- function(df1, df2, varname) {
dist_matrix <- st_distance(df1, df2) %>%
drop_units()
df1[,varname] <- rowMins(dist_matrix)
return(df1)
}
num_radius <- function(df1, df2, varname, radius) {
dist_matrix <- st_distance(df1, df2) %>%
drop_units() %>%
as.data.frame()
df1[,varname] <- rowSums(dist_matrix <= radius)
return(df1)
}With these, we can do our calculations all at once.
# resale_full_details_2021_22_sf <-
# proximity(resale_prices_2021_22_sf, downtown_core_centroid_sf, "PROX_CBD") %>%
# proximity(., eldercare, "PROX_ELDERCARE") %>%
# proximity(., hawker_centre, "PROX_HAWKER_CENTRE") %>%
# proximity(., mrt_exit, "PROX_MRT") %>%
# proximity(., parks, "PROX_PARK") %>%
# proximity(., top_pri_sch, "PROX_GOOD_PRI_SCH") %>%
# proximity(., malls, "PROX_MALL") %>%
# proximity(., supermarkets, "PROX_SUPERMARKET")
#
# resale_full_details_2023_sf <-
# proximity(resale_prices_2023_sf, downtown_core_centroid_sf, "PROX_CBD") %>%
# proximity(., eldercare, "PROX_ELDERCARE") %>%
# proximity(., hawker_centre, "PROX_HAWKER_CENTRE") %>%
# proximity(., mrt_exit, "PROX_MRT") %>%
# proximity(., parks, "PROX_PARK") %>%
# proximity(., top_pri_sch, "PROX_GOOD_PRI_SCH") %>%
# proximity(., malls, "PROX_MALL") %>%
# proximity(., supermarkets, "PROX_SUPERMARKET")# resale_full_details_2021_22_sf <-
# num_radius(resale_prices_2021_22_sf, kindergartens, "NUM_KINDERGARTEN", 350) %>%
# num_radius(., childcare, "NUM_CHILDCARE", 350) %>%
# num_radius(., bus_stops, "NUM_BUS_STOP", 350) %>%
# num_radius(., pri_schs, "NUM_PRI_SCH", 1000)
#
# resale_full_details_2023_sf <-
# num_radius(resale_prices_2023_sf, kindergartens, "NUM_KINDERGARTEN", 350) %>%
# num_radius(., childcare, "NUM_CHILDCARE", 350) %>%
# num_radius(., bus_stops, "NUM_BUS_STOP", 350) %>%
# num_radius(., pri_schs, "NUM_PRI_SCH", 1000)Since these calculations take a while to load, lets save and load everything from RDS.
# saveRDS(resale_full_details_2021_22_sf, file="data/rds/resale_full_details_2021_22_sf.rds")
# saveRDS(resale_full_details_2023_sf, file="data/rds/resale_full_details_2023_sf.rds")
resale_full_details_2021_22_sf <- read_rds("data/rds/resale_full_details_2021_22_sf.rds")
resale_full_details_2023_sf <- read_rds("data/rds/resale_full_details_2023_sf.rds")Data Preparation
Before we start on our linear regression, we first need to transform our data into an appropriate format that the model for the regression model to interpret. As such, we will be changing all our categorical variables into numerical variables via encoding.
Encoding Variables
Let us first look at what we are working with.
glimpse(resale_full_details_2021_22_sf)Rows: 55,817
Columns: 24
$ month <chr> "2021-01", "2021-01", "2021-01", "2021-01", "2021-…
$ town <chr> "ANG MO KIO", "ANG MO KIO", "ANG MO KIO", "ANG MO …
$ flat_type <chr> "2 ROOM", "2 ROOM", "3 ROOM", "3 ROOM", "3 ROOM", …
$ block <chr> "170", "170", "331", "534", "561", "170", "463", "…
$ street_name <chr> "ANG MO KIO AVE 4", "ANG MO KIO AVE 4", "ANG MO KI…
$ storey_range <chr> "01 TO 03", "07 TO 09", "04 TO 06", "04 TO 06", "0…
$ floor_area_sqm <dbl> 45, 45, 68, 68, 68, 60, 68, 68, 60, 73, 67, 67, 68…
$ flat_model <chr> "Improved", "Improved", "New Generation", "New Gen…
$ lease_commence_date <dbl> 1986, 1986, 1981, 1980, 1980, 1986, 1980, 1981, 19…
$ remaining_lease <chr> "64 years 01 month", "64 years 01 month", "59 year…
$ resale_price <dbl> 211000, 225000, 260000, 265000, 265000, 268000, 26…
$ geometry <POINT [m]> POINT (28346.43 39555.53), POINT (28346.43 3…
$ PROX_CBD <dbl> 101793.46, 101793.46, 100092.40, 99828.46, 99384.9…
$ PROX_ELDERCARE <dbl> 429.68375, 429.68375, 412.40581, 1008.60569, 683.4…
$ PROX_HAWKER_CENTRE <dbl> 314.3604, 314.3604, 356.0478, 146.7193, 307.8475, …
$ PROX_MRT <dbl> 73.66065, 73.66065, 818.28864, 668.50386, 889.4625…
$ PROX_PARK <dbl> 303.1924, 303.1924, 358.0379, 554.3379, 817.5539, …
$ PROX_GOOD_PRI_SCH <dbl> 262.1063, 262.1063, 957.1154, 409.3479, 602.7432, …
$ PROX_MALL <dbl> 1439.9090, 1439.9090, 826.9463, 829.6281, 1012.796…
$ PROX_SUPERMARKET <dbl> 3.413032e+02, 3.413032e+02, 4.369613e+02, 1.592391…
$ NUM_KINDERGARTEN <dbl> 1, 1, 1, 1, 1, 1, 2, 1, 1, 0, 2, 1, 0, 1, 0, 2, 1,…
$ NUM_CHILDCARE <dbl> 4, 4, 2, 2, 4, 4, 5, 2, 4, 2, 3, 2, 2, 2, 3, 4, 2,…
$ NUM_BUS_STOP <dbl> 3, 3, 7, 11, 8, 3, 6, 9, 3, 4, 5, 4, 6, 9, 9, 5, 4…
$ NUM_PRI_SCH <dbl> 3, 3, 3, 4, 4, 3, 5, 3, 3, 1, 3, 2, 3, 5, 2, 3, 2,…While all our freshly calculated data looks good, we can see some of the variables from our resale dataset still need to further processed, namely storey_range and remaining_lease. We also have to use lease_commence_date and month in order to determine the age of the unit.
Remaining lease is the easiest to fix, we can simplify it to just the number of years left, and cast it to a number.
resale_full_details_2021_22_sf$remaining_lease <- as.numeric(
word(resale_full_details_2021_22_sf$remaining_lease, 1))
resale_full_details_2023_sf$remaining_lease <- as.numeric(
word(resale_full_details_2023_sf$remaining_lease, 1))Storey Range is slightly more difficult, as we will have to transform the range into an ordinal variable.
unique(resale_full_details_2021_22_sf$storey_range) [1] "01 TO 03" "07 TO 09" "04 TO 06" "10 TO 12" "13 TO 15" "16 TO 18"
[7] "19 TO 21" "22 TO 24" "28 TO 30" "25 TO 27" "34 TO 36" "31 TO 33"
[13] "37 TO 39" "43 TO 45" "40 TO 42" "46 TO 48" "49 TO 51"However, we can see that the storey ranges fall very nicely into ranges of 3. As such, we can transform them into ordinal values by taking the last word in the string, converting it into a number, then dividing by 3.
resale_full_details_2021_22_sf$storey_range <- (as.numeric(
word(resale_full_details_2021_22_sf$storey_range, -1)) / 3)
resale_full_details_2023_sf$storey_range <- (as.numeric(
word(resale_full_details_2023_sf$storey_range, -1)) / 3)Lastly, we have the Age of Unit to calculate. We can get this value in years by taking the month minus the lease_commence_date.
resale_full_details_2021_22_sf <- resale_full_details_2021_22_sf %>%
add_column(age_of_unit = NA) %>%
mutate(age_of_unit = (
as.numeric(substr(resale_full_details_2021_22_sf$month, 1, 4)) -
as.numeric(resale_full_details_2021_22_sf$lease_commence_date)))
resale_full_details_2023_sf <- resale_full_details_2023_sf %>%
add_column(age_of_unit = NA) %>%
mutate(age_of_unit = (
as.numeric(substr(resale_full_details_2023_sf$month, 1, 4)) -
as.numeric(resale_full_details_2023_sf$lease_commence_date)))Let’s just double check that all our calculations went well:
sum(is.na(resale_full_details_2021_22_sf$age_of_unit))[1] 0sum(is.na(resale_full_details_2023_sf$age_of_unit))[1] 0Separate into Sub-Markets
Now that we have encoded all the necessary values, we can drop all other columns. However, before we do this, we need to separate our data into our 3 sub-markets of interest: 3-room, 4-room and 5-room flats.
three_room_2021_22_sf <- resale_full_details_2021_22_sf %>%
filter(flat_type == '3 ROOM')
four_room_2021_22_sf <- resale_full_details_2021_22_sf %>%
filter(flat_type == '4 ROOM')
five_room_2021_22_sf <- resale_full_details_2021_22_sf %>%
filter(flat_type == '5 ROOM')
three_room_2023_sf <- resale_full_details_2023_sf %>%
filter(flat_type == '3 ROOM')
four_room_2023_sf <- resale_full_details_2023_sf %>%
filter(flat_type == '4 ROOM')
five_room_2023_sf <- resale_full_details_2023_sf %>%
filter(flat_type == '5 ROOM')Remove Unnecessary Columns
Now that we have encoded all the necessary values, we can drop all other columns before saving this to rds for us to work on in our regression section later.
three_room_2021_22_sf <- three_room_2021_22_sf %>%
dplyr::select(c(6:7, 10:25))
four_room_2021_22_sf <- four_room_2021_22_sf %>%
dplyr::select(c(6:7, 10:25))
five_room_2021_22_sf <- five_room_2021_22_sf %>%
dplyr::select(c(6:7, 10:25))
three_room_2023_sf <- three_room_2023_sf %>%
dplyr::select(c(6:7, 10:25))
four_room_2023_sf <- four_room_2023_sf %>%
dplyr::select(c(6:7, 10:25))
five_room_2023_sf <- five_room_2023_sf %>%
dplyr::select(c(6:7, 10:25))# saveRDS(three_room_2021_22_sf, file="data/rds/three_room_2021_22_sf.rds")
# saveRDS(four_room_2021_22_sf, file="data/rds/four_room_2021_22_sf.rds")
# saveRDS(five_room_2021_22_sf, file="data/rds/five_room_2021_22_sf.rds")
#
# saveRDS(three_room_2023_sf, file="data/rds/three_room_2023_sf.rds")
# saveRDS(four_room_2023_sf, file="data/rds/four_room_2023_sf.rds")
# saveRDS(five_room_2023_sf, file="data/rds/five_room_2023_sf.rds")
three_room_2021_22_sf <- read_rds("data/rds/three_room_2021_22_sf.rds")
four_room_2021_22_sf <- read_rds("data/rds/four_room_2021_22_sf.rds")
five_room_2021_22_sf <- read_rds("data/rds/five_room_2021_22_sf.rds")
three_room_2023_sf <- read_rds("data/rds/three_room_2023_sf.rds")
four_room_2023_sf <- read_rds("data/rds/four_room_2023_sf.rds")
five_room_2023_sf <- read_rds("data/rds/five_room_2023_sf.rds")Exploratory Data Analysis
Statistical Visualisation
Resale Price
Before we jump into our analysis, let us first do some visualization on our test data, starting with our resale prices.
# Remove scientific notation from our graphs
options(scipen = 999)ggplot(data=three_room_2021_22_sf, aes(x=`resale_price`)) +
geom_histogram(bins=20, color="black", fill="pink") +
labs(title = "Distribution of Resale Prices for 3 Room Flats (2021 - 2022)",
x = "Resale Prices",
y = 'Frequency') +
scale_x_continuous(labels = scales::comma) +
scale_y_continuous(labels = scales::comma)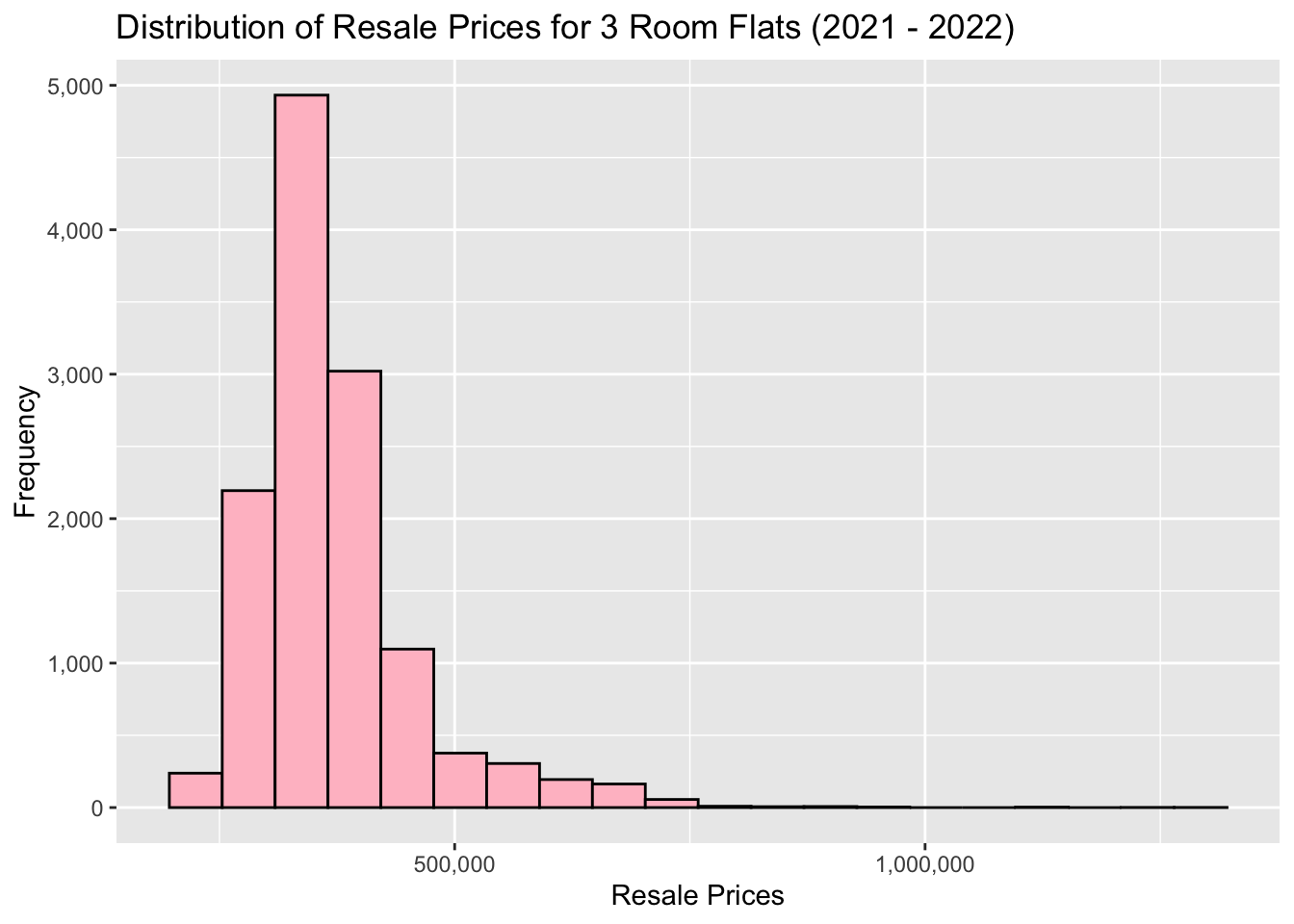
ggplot(data = three_room_2021_22_sf, aes(x = '', y = resale_price)) +
geom_boxplot() +
labs(x='', y='3 Room Resale Flat Prices')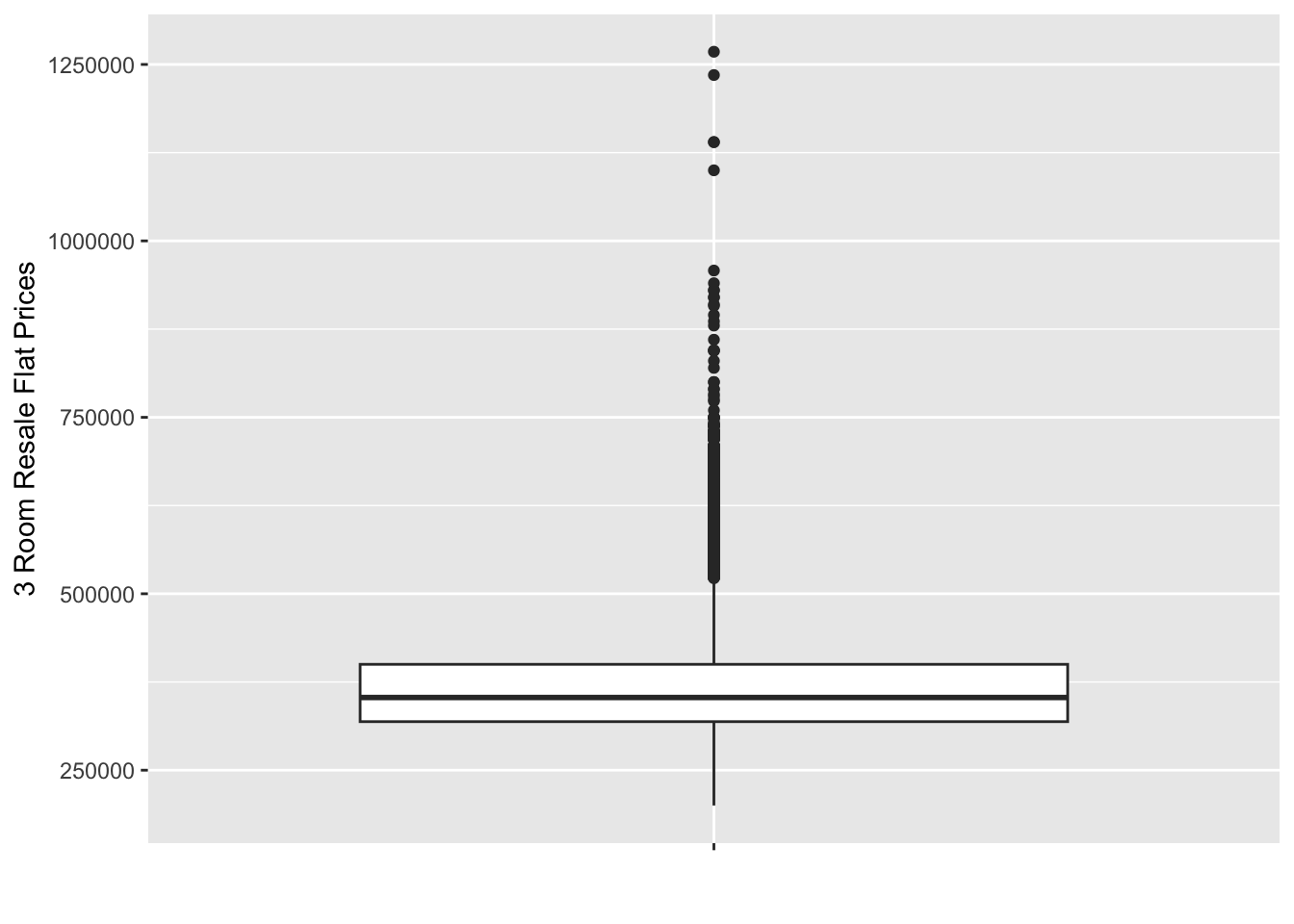
ggplot(data=four_room_2021_22_sf, aes(x=`resale_price`)) +
geom_histogram(bins=20, color="black", fill="pink") +
labs(title = "Distribution of Resale Prices for 3 Room Flats (2021 - 2022)",
x = "Resale Prices",
y = 'Frequency') +
scale_x_continuous(labels = scales::comma) +
scale_y_continuous(labels = scales::comma)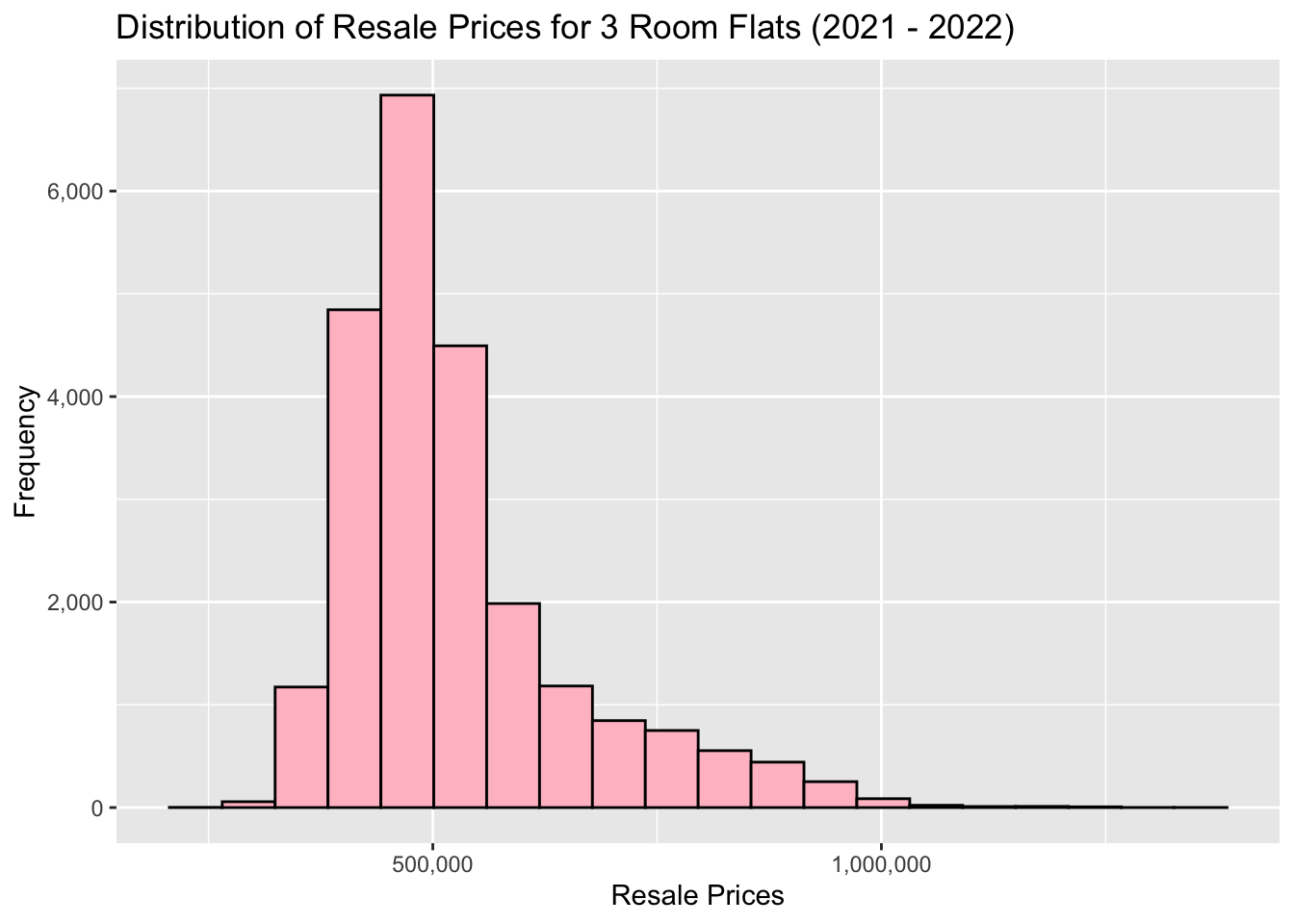
ggplot(data = four_room_2021_22_sf, aes(x = '', y = resale_price)) +
geom_boxplot() +
labs(x='', y='3 Room Resale Flat Prices')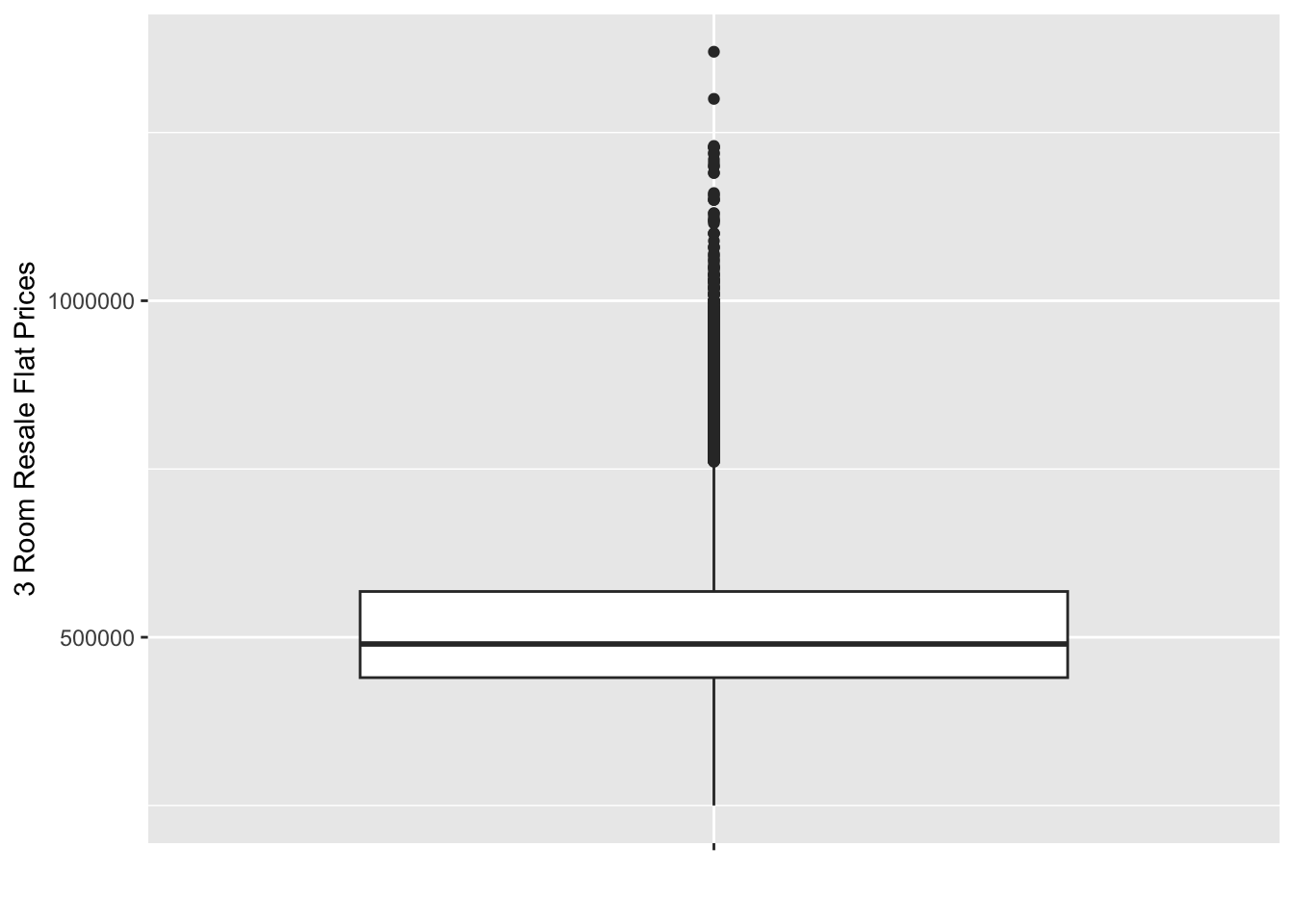
ggplot(data=five_room_2021_22_sf, aes(x=`resale_price`)) +
geom_histogram(bins=20, color="black", fill="pink") +
labs(title = "Distribution of Resale Prices for 3 Room Flats (2021 - 2022)",
x = "Resale Prices",
y = 'Frequency') +
scale_x_continuous(labels = scales::comma) +
scale_y_continuous(labels = scales::comma)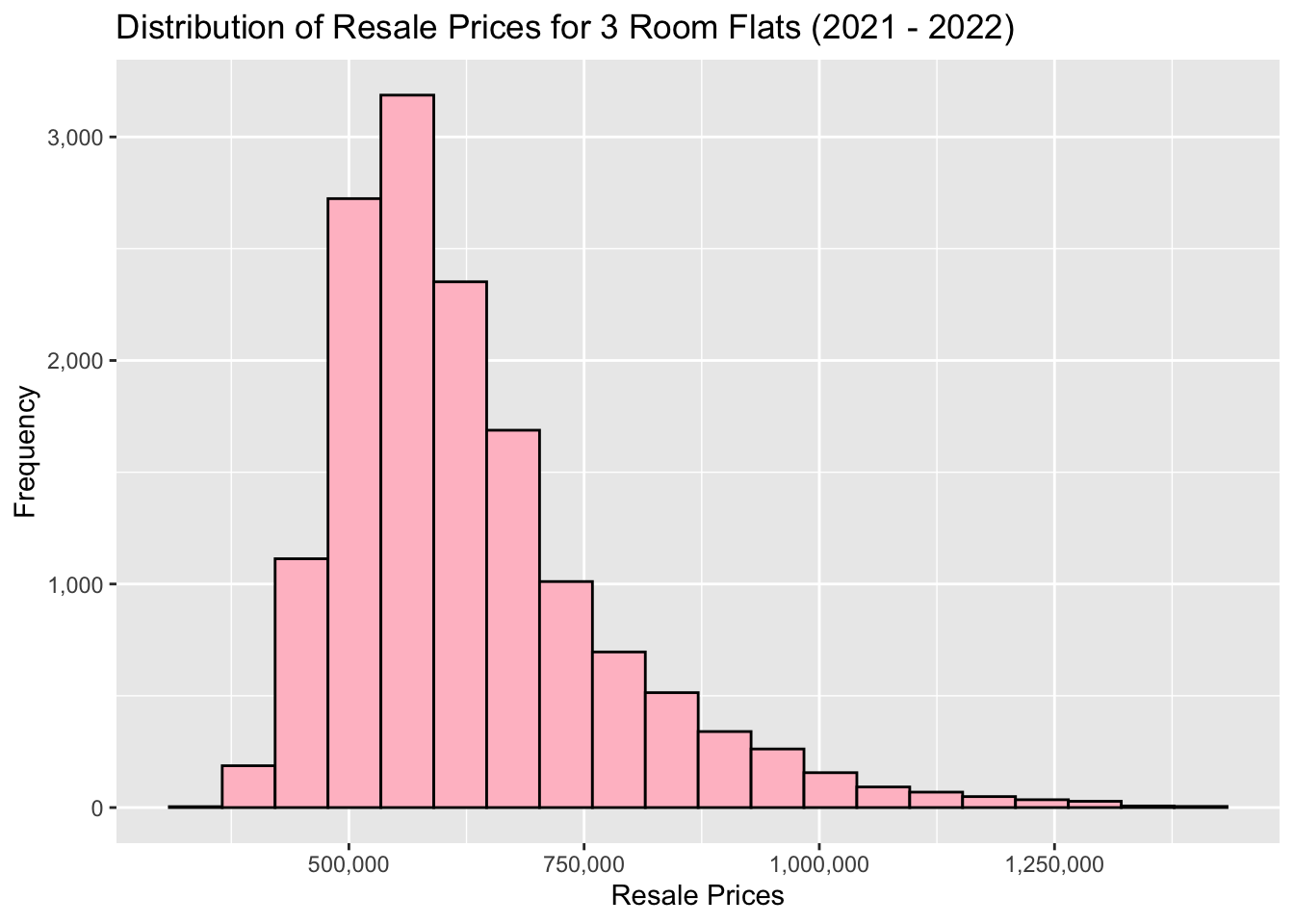
ggplot(data = five_room_2021_22_sf, aes(x = '', y = resale_price)) +
geom_boxplot() +
labs(x='', y='3 Room Resale Flat Prices')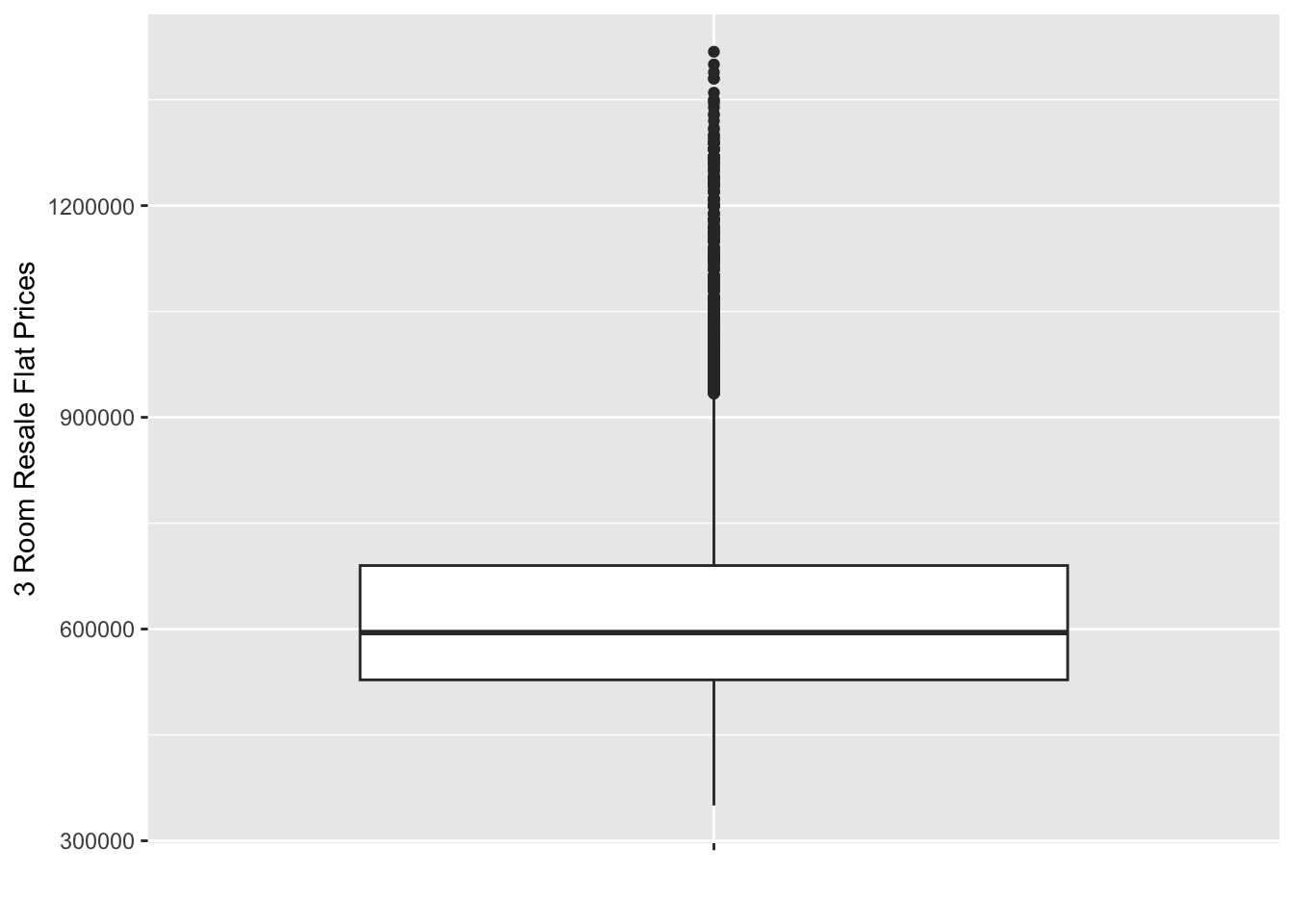
As we can see, all 3 have an distinct right skew. This indicates that more resale flats were bought at relatively lower price.
From both our histograms and boxplots, we can also see the mode of the data increasing gradually as we move from 3 to 4 to 5 rooms. This aligns with out expectations, as a flat with more rooms should on average cost more than one with fewer.
Although we do see quite a lot of outliers in our boxplots (with the highest prices being well over 2-3 times the mean price), in general we see that 3 room flats being in about the 300k - 400k range, 4 room flats being in the 450k-550k range, and 5 rooms flats in the 500k-700k range.
Flat Factors
Let us look at the distribution of our Resale Flat factors, namely floor_area_sqm, storey_range, remaining_lease and age_of_unit.
floor_area_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `floor_area_sqm`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
storey_range_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `storey_range`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
remaining_lease_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `remaining_lease`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
unit_age_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `age_of_unit`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(floor_area_plot, storey_range_plot, remaining_lease_plot, unit_age_plot, ncol = 2, nrow = 2)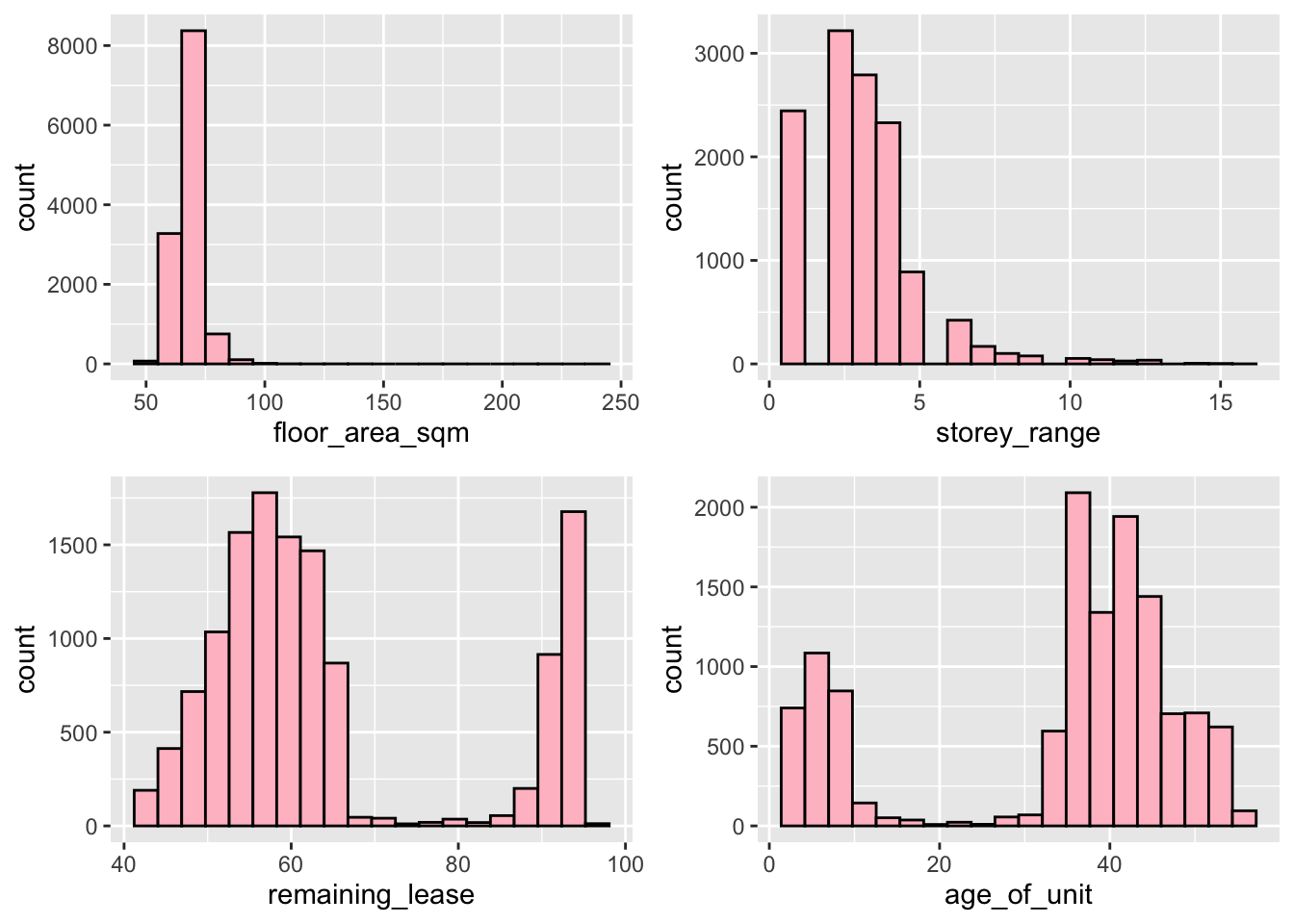
floor_area_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `floor_area_sqm`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
storey_range_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `storey_range`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
remaining_lease_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `remaining_lease`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
unit_age_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `age_of_unit`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(floor_area_plot, storey_range_plot, remaining_lease_plot, unit_age_plot, ncol = 2, nrow = 2)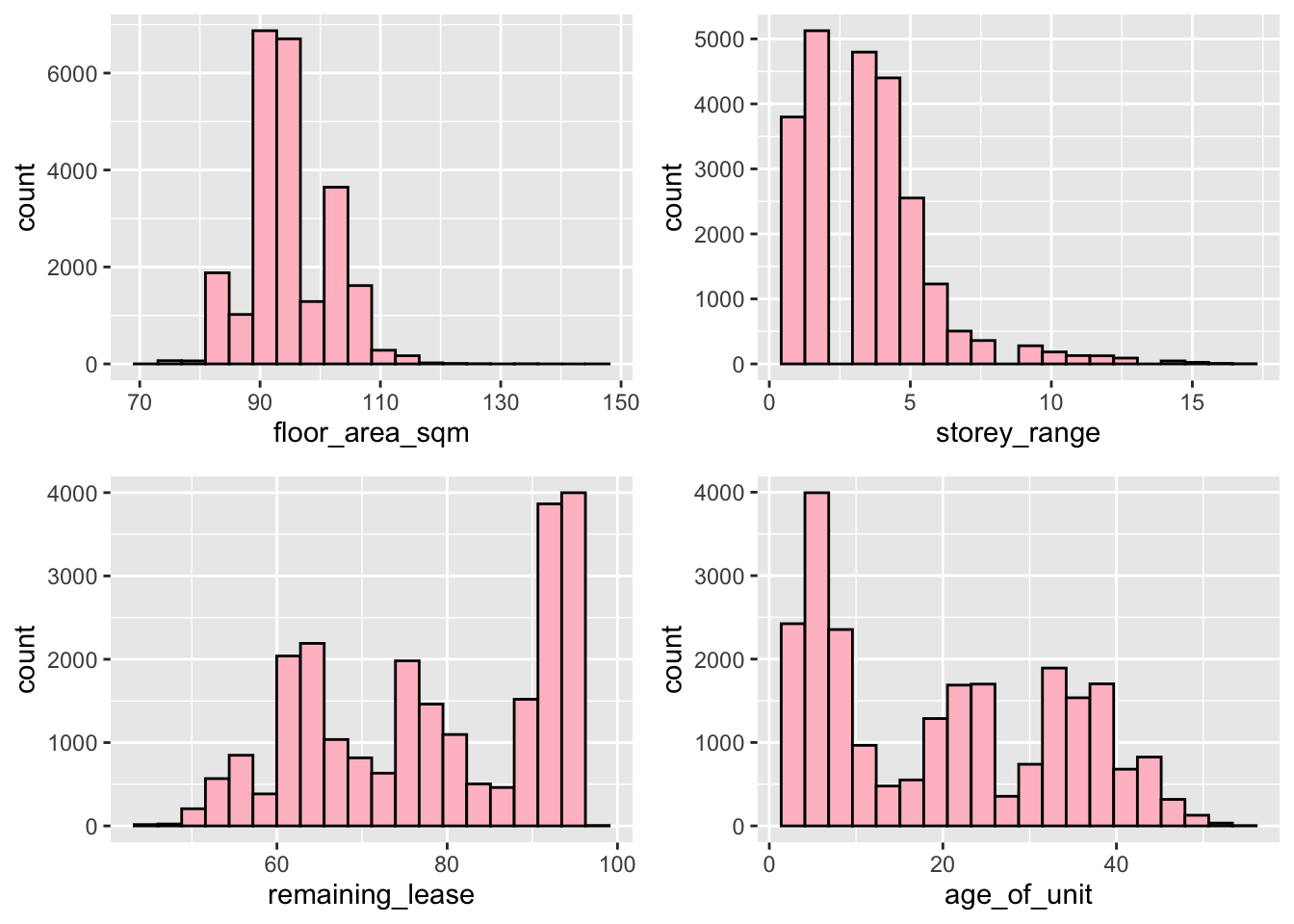
floor_area_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `floor_area_sqm`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
storey_range_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `storey_range`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
remaining_lease_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `remaining_lease`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
unit_age_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `age_of_unit`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(floor_area_plot, storey_range_plot, remaining_lease_plot, unit_age_plot, ncol = 2, nrow = 2)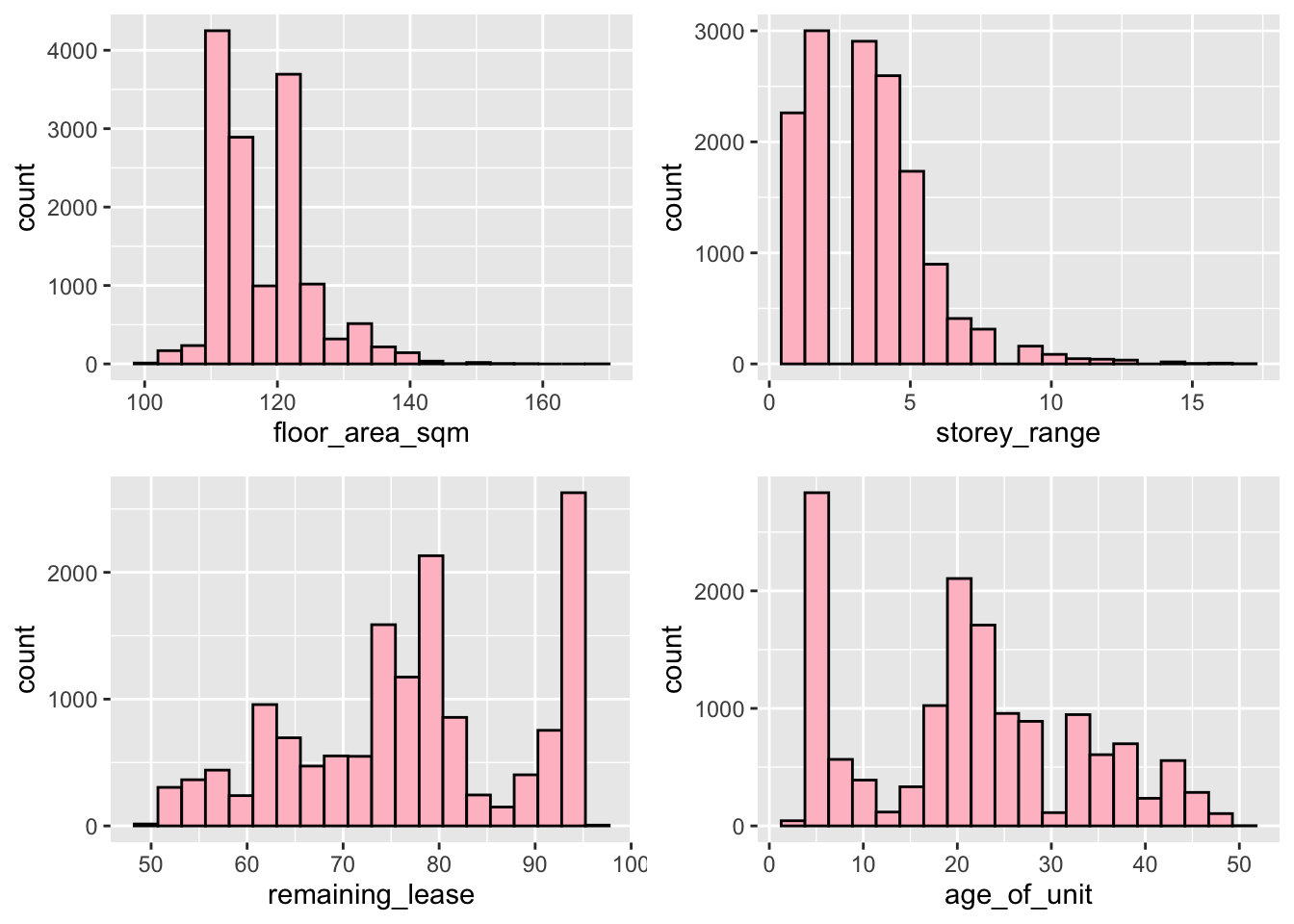
Locational Factors
And lastly, we can visualise our locational factors; PROX_CBD, PROX_ELDERCARE, PROX_HAWKER_CENTRE, PROX_MRT, PROX_PARK, PROX_GOOD_PRI_SCH, PROX_MALL, PROX_SUPERMARKET, NUM_KINDERGARTEN, NUM_CHILDCARE, NUM_BUS_STOP and NUM_PRI_SCH.
PROX_CBD_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `PROX_CBD`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_ELDERCARE_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `PROX_ELDERCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_HAWKER_CENTRE_plot <- ggplot(data = three_room_2021_22_sf,
aes(x = `PROX_HAWKER_CENTRE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MRT_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `PROX_MRT`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_PARK_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `PROX_PARK`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_GOOD_PRI_SCH_plot <- ggplot(data = three_room_2021_22_sf,
aes(x = `PROX_GOOD_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MALL_plot <- ggplot(data = three_room_2021_22_sf,
aes(x = `PROX_MALL`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_SUPERMARKET_plot <- ggplot(data = three_room_2021_22_sf,
aes(x = `PROX_SUPERMARKET`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_KINDERGARTEN_plot <- ggplot(data = three_room_2021_22_sf,
aes(x = `NUM_KINDERGARTEN`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_CHILDCARE_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `NUM_CHILDCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_BUS_STOP_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `NUM_BUS_STOP`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_PRI_SCH_plot <- ggplot(data = three_room_2021_22_sf, aes(x = `NUM_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(PROX_CBD_plot, PROX_ELDERCARE_plot, PROX_HAWKER_CENTRE_plot, PROX_MRT_plot,
PROX_PARK_plot, PROX_GOOD_PRI_SCH_plot, PROX_MALL_plot,
PROX_SUPERMARKET_plot, NUM_KINDERGARTEN_plot, NUM_CHILDCARE_plot,
NUM_BUS_STOP_plot, NUM_PRI_SCH_plot, ncol = 3, nrow = 4)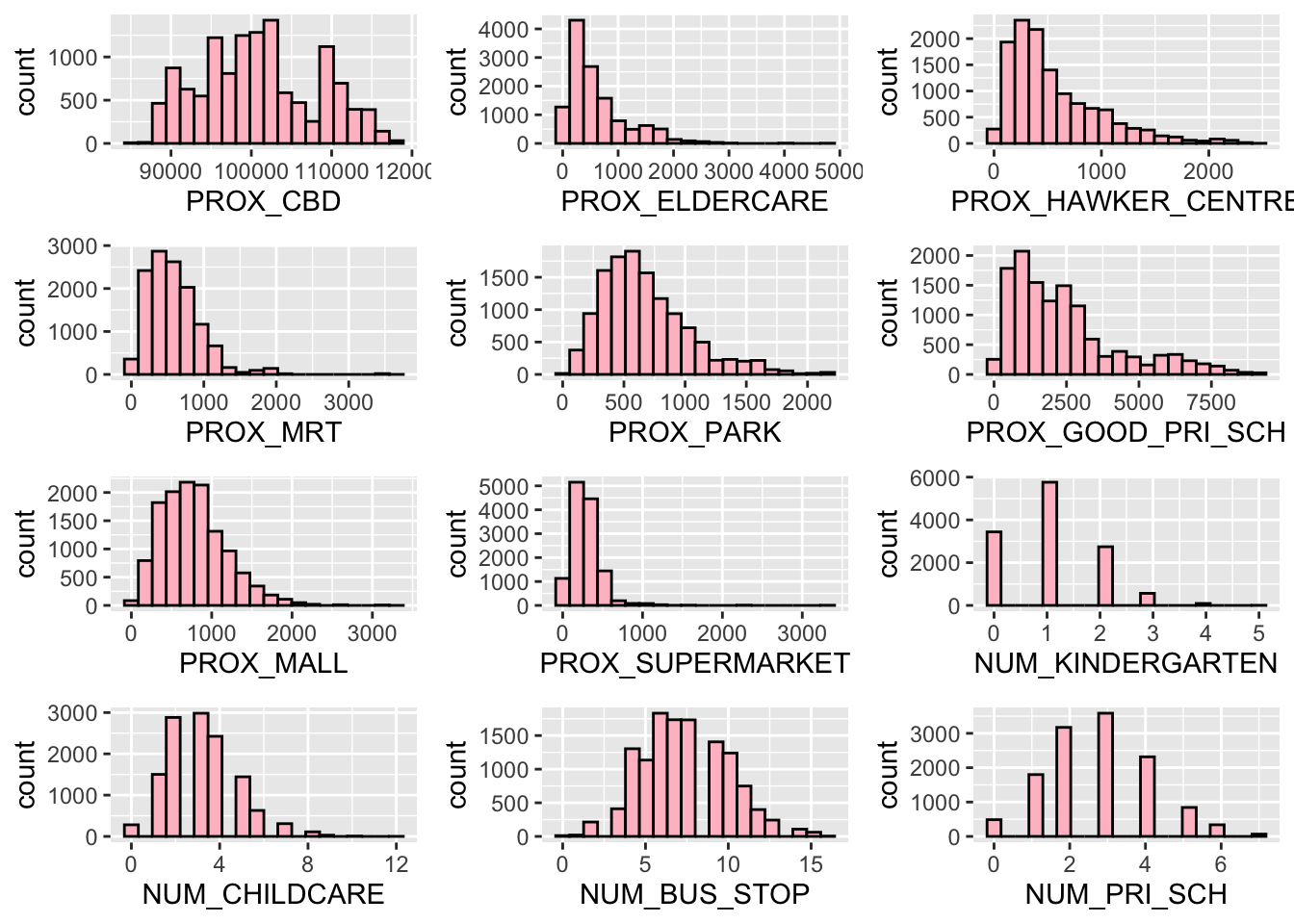
PROX_CBD_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `PROX_CBD`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_ELDERCARE_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `PROX_ELDERCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_HAWKER_CENTRE_plot <- ggplot(data = four_room_2021_22_sf,
aes(x = `PROX_HAWKER_CENTRE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MRT_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `PROX_MRT`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_PARK_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `PROX_PARK`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_GOOD_PRI_SCH_plot <- ggplot(data = four_room_2021_22_sf,
aes(x = `PROX_GOOD_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MALL_plot <- ggplot(data = four_room_2021_22_sf,
aes(x = `PROX_MALL`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_SUPERMARKET_plot <- ggplot(data = four_room_2021_22_sf,
aes(x = `PROX_SUPERMARKET`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_KINDERGARTEN_plot <- ggplot(data = four_room_2021_22_sf,
aes(x = `NUM_KINDERGARTEN`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_CHILDCARE_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `NUM_CHILDCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_BUS_STOP_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `NUM_BUS_STOP`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_PRI_SCH_plot <- ggplot(data = four_room_2021_22_sf, aes(x = `NUM_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(PROX_CBD_plot, PROX_ELDERCARE_plot, PROX_HAWKER_CENTRE_plot, PROX_MRT_plot,
PROX_PARK_plot, PROX_GOOD_PRI_SCH_plot, PROX_MALL_plot,
PROX_SUPERMARKET_plot, NUM_KINDERGARTEN_plot, NUM_CHILDCARE_plot,
NUM_BUS_STOP_plot, NUM_PRI_SCH_plot, ncol = 3, nrow = 4)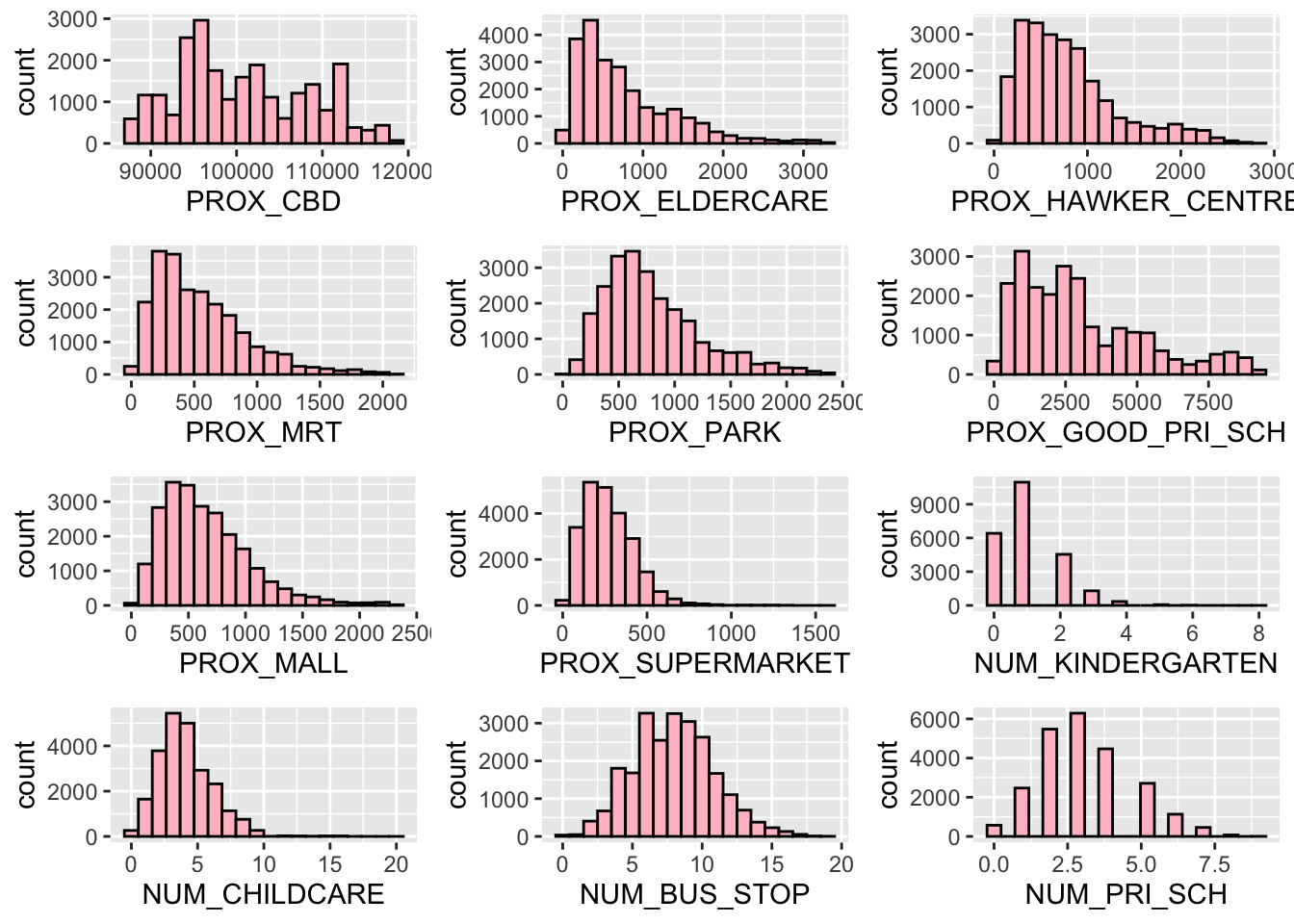
PROX_CBD_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `PROX_CBD`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_ELDERCARE_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `PROX_ELDERCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_HAWKER_CENTRE_plot <- ggplot(data = five_room_2021_22_sf,
aes(x = `PROX_HAWKER_CENTRE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MRT_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `PROX_MRT`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_PARK_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `PROX_PARK`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_GOOD_PRI_SCH_plot <- ggplot(data = five_room_2021_22_sf,
aes(x = `PROX_GOOD_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_MALL_plot <- ggplot(data = five_room_2021_22_sf,
aes(x = `PROX_MALL`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
PROX_SUPERMARKET_plot <- ggplot(data = five_room_2021_22_sf,
aes(x = `PROX_SUPERMARKET`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_KINDERGARTEN_plot <- ggplot(data = five_room_2021_22_sf,
aes(x = `NUM_KINDERGARTEN`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_CHILDCARE_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `NUM_CHILDCARE`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_BUS_STOP_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `NUM_BUS_STOP`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
NUM_PRI_SCH_plot <- ggplot(data = five_room_2021_22_sf, aes(x = `NUM_PRI_SCH`)) +
geom_histogram(bins=20, color="black", fill = 'pink')
ggarrange(PROX_CBD_plot, PROX_ELDERCARE_plot, PROX_HAWKER_CENTRE_plot, PROX_MRT_plot,
PROX_PARK_plot, PROX_GOOD_PRI_SCH_plot, PROX_MALL_plot,
PROX_SUPERMARKET_plot, NUM_KINDERGARTEN_plot, NUM_CHILDCARE_plot,
NUM_BUS_STOP_plot, NUM_PRI_SCH_plot, ncol = 3, nrow = 4)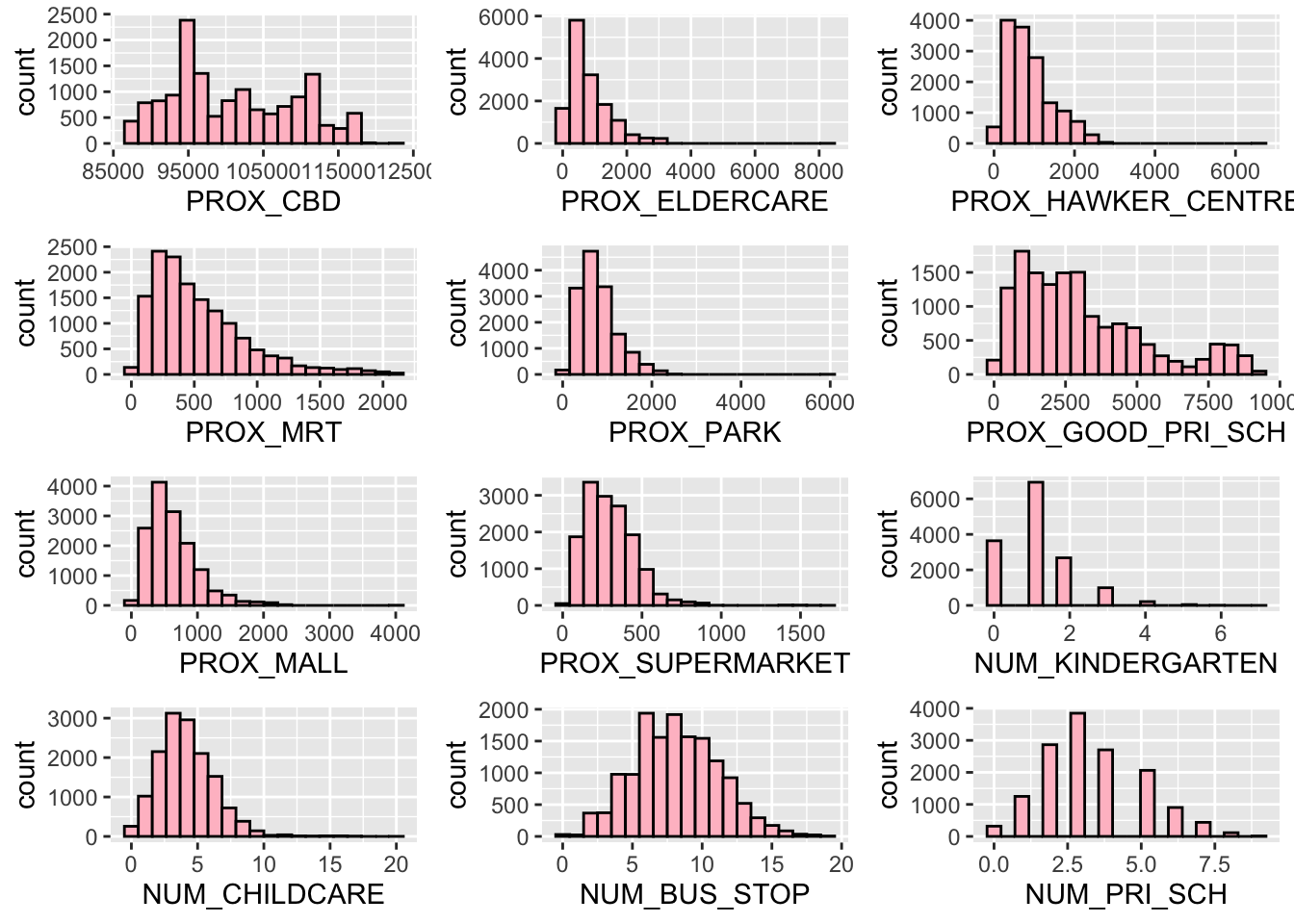
Spatial Visualisation
Let us quickly revisit the spatial visualisation of our resale price data.
tmap_mode("view")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(three_room_2021_22_sf)+
tm_dots(col = "resale_price",
size = 0.01,
border.col = "black",
border.lwd = 0.5) +
tmap_options(check.and.fix = TRUE) +
tm_view(set.zoom.limits = c(11, 16))tmap_mode("view")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(four_room_2021_22_sf)+
tm_dots(col = "resale_price",
size = 0.01,
border.col = "black",
border.lwd = 0.5) +
tmap_options(check.and.fix = TRUE) +
tm_view(set.zoom.limits = c(11, 16))tmap_mode("view")
tm_shape(mpsz) +
tm_polygons() +
tm_shape(five_room_2021_22_sf)+
tm_dots(col = "resale_price",
size = 0.01,
border.col = "black",
border.lwd = 0.5) +
tmap_options(check.and.fix = TRUE) +
tm_view(set.zoom.limits = c(11, 16))From both our statistical and spatial visualisations, we can see that our 4 room flat dataset is the richest both in terms of the amount of data, as well as the distribution of data. As such, we will be focusing on 4 room flats for our machine learning models.
Correlation Matrix
Before we start any model training, let us check for any multicolinearity in our 4 room data set. To do this, we will be using a correlation matrix to visualise the relationship between each pair of factors.
four_room_nogeo <- four_room_2021_22_sf %>% st_drop_geometry()
corrplot(cor(four_room_nogeo),
diag = FALSE,
order = "AOE",
tl.pos = "td",
tl.cex = 0.5,
method = "number",
type = "upper")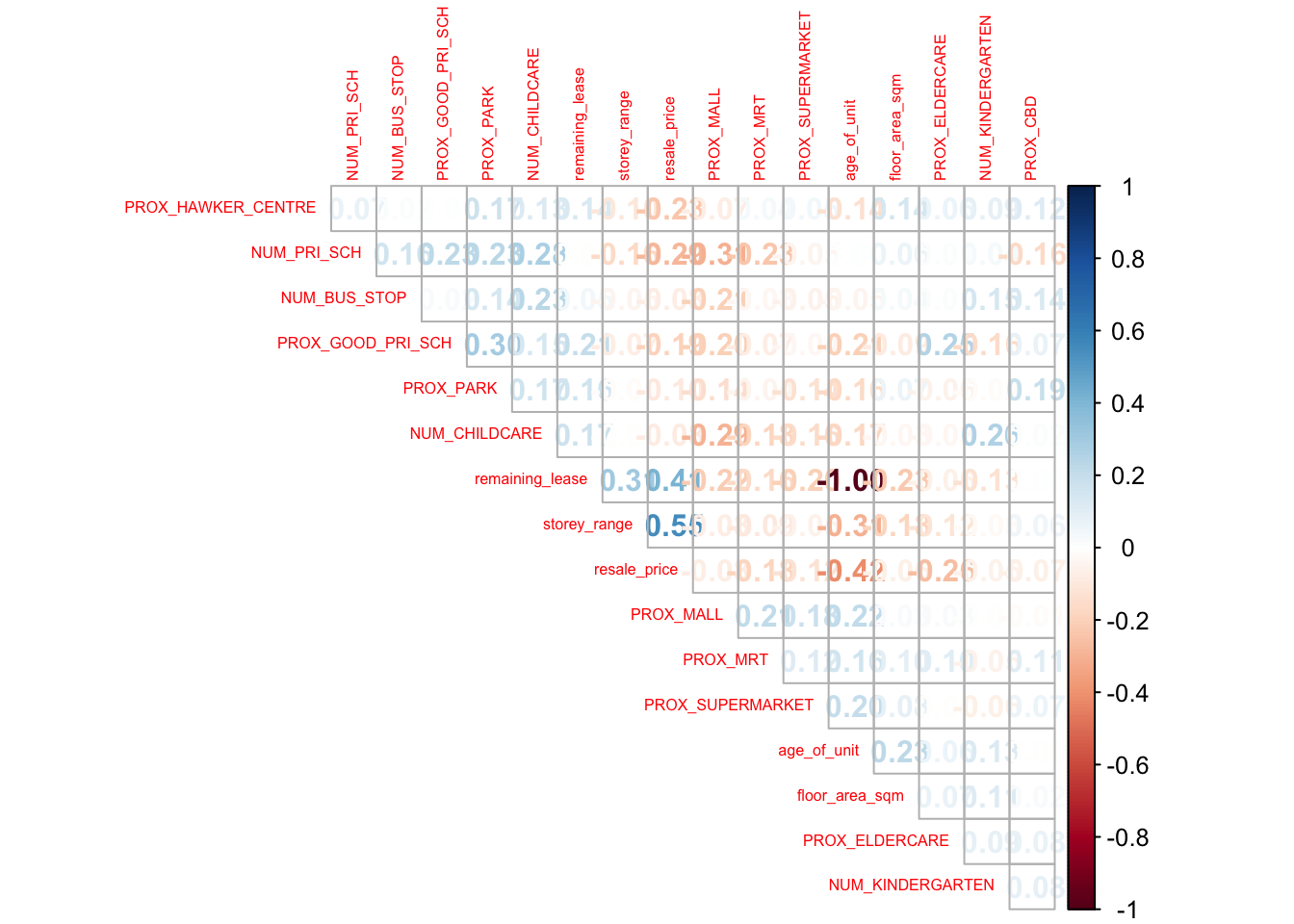
From this correlation plot, we can see that all our factors have a relatively low correlation (less than 0.6 and greater than -0.6) except for remaining_lease and age_of_unit, which have an extremely negative correlation of -1. This makes sense, as typically all HDB flats have a 99 year lease and therefore the age of the flat would be directly related to the remaining lease (would add up to 99, and therefore have a negative relationship with each other).
We must therefore remove one of these two factors. We will be removing the age_of_unit.
train_data <- four_room_2021_22_sf %>%
dplyr::select(, 0:17)
test_data <- four_room_2023_sf %>%
dplyr::select(, 0:17)saveRDS(train_data, file="data/rds/train_data.rds")
saveRDS(test_data, file="data/rds/test_data.rds")Predictive Model Training
Now that we have finished all that preprocessing, we can finally move on to the our model training. We will be training predictive models with 3 different methods, namely Multiple Linear Regression, Random Forest, and Geographically Weighted Random Forest.
First, let us load in our training and testing data from rds.
train_data <- read_rds("data/rds/train_data.rds")
test_data <- read_rds("data/rds/test_data.rds")Multiple Linear Regression
Let us first train a simple multiple linear regression, with resale price being our variable to predict.
# price_mlr <- lm(resale_price ~ floor_area_sqm +
# storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN +
# NUM_CHILDCARE + NUM_BUS_STOP +
# NUM_PRI_SCH,
# data=train_data)# write_rds(price_mlr, "data/model/price_mlr.rds" )
price_mlr <- read_rds("data/model/price_mlr.rds")summary(price_mlr)
Call:
lm(formula = resale_price ~ floor_area_sqm + storey_range + remaining_lease +
PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE + PROX_MRT +
PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL + PROX_SUPERMARKET +
NUM_KINDERGARTEN + NUM_CHILDCARE + NUM_BUS_STOP + NUM_PRI_SCH,
data = train_data)
Residuals:
Min 1Q Median 3Q Max
-446088 -52126 -4264 47958 475641
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 263417.95635 12436.32072 21.181 < 0.0000000000000002 ***
floor_area_sqm 2693.33446 85.65820 31.443 < 0.0000000000000002 ***
storey_range 21484.90803 276.47442 77.710 < 0.0000000000000002 ***
remaining_lease 3402.54398 47.75189 71.255 < 0.0000000000000002 ***
PROX_CBD -0.97112 0.07832 -12.400 < 0.0000000000000002 ***
PROX_ELDERCARE -29.83367 0.97251 -30.677 < 0.0000000000000002 ***
PROX_HAWKER_CENTRE -53.90901 1.12631 -47.863 < 0.0000000000000002 ***
PROX_MRT -47.21443 1.61322 -29.267 < 0.0000000000000002 ***
PROX_PARK -10.25360 1.47059 -6.972 0.0000000000031964 ***
PROX_GOOD_PRI_SCH -7.88571 0.29494 -26.736 < 0.0000000000000002 ***
PROX_MALL -27.61043 1.65562 -16.677 < 0.0000000000000002 ***
PROX_SUPERMARKET -23.72765 3.84306 -6.174 0.0000000006760400 ***
NUM_KINDERGARTEN 3880.35001 644.85053 6.017 0.0000000017980339 ***
NUM_CHILDCARE -4945.07940 322.00765 -15.357 < 0.0000000000000002 ***
NUM_BUS_STOP -1534.47450 204.05269 -7.520 0.0000000000000567 ***
NUM_PRI_SCH -19005.23870 426.66327 -44.544 < 0.0000000000000002 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 84970 on 23640 degrees of freedom
Multiple R-squared: 0.5698, Adjusted R-squared: 0.5695
F-statistic: 2088 on 15 and 23640 DF, p-value: < 0.00000000000000022As we can see, all of our independent variables are statistically significant. This way, we know that our model is appropriate as all our independent variables do indeed have an effect on the price, and we do not need to make any changes to our input data.
ols_regress(price_mlr) Model Summary
----------------------------------------------------------------------
R 0.755 RMSE 84966.679
R-Squared 0.570 Coef. Var 16.150
Adj. R-Squared 0.570 MSE 7219336600.895
Pred R-Squared 0.569 MAE 64457.781
----------------------------------------------------------------------
RMSE: Root Mean Square Error
MSE: Mean Square Error
MAE: Mean Absolute Error
ANOVA
-------------------------------------------------------------------------------------------
Sum of
Squares DF Mean Square F Sig.
-------------------------------------------------------------------------------------------
Regression 226062121142929.219 15 15070808076195.281 2087.561 0.0000
Residual 170665117245150.469 23640 7219336600.895
Total 396727238388079.688 23655
-------------------------------------------------------------------------------------------
Parameter Estimates
------------------------------------------------------------------------------------------------------------
model Beta Std. Error Std. Beta t Sig lower upper
------------------------------------------------------------------------------------------------------------
(Intercept) 263417.956 12436.321 21.181 0.000 239041.968 287793.945
floor_area_sqm 2693.334 85.658 0.143 31.443 0.000 2525.439 2861.230
storey_range 21484.908 276.474 0.366 77.710 0.000 20943.000 22026.816
remaining_lease 3402.544 47.752 0.360 71.255 0.000 3308.947 3496.141
PROX_CBD -0.971 0.078 -0.057 -12.400 0.000 -1.125 -0.818
PROX_ELDERCARE -29.834 0.973 -0.141 -30.677 0.000 -31.740 -27.927
PROX_HAWKER_CENTRE -53.909 1.126 -0.219 -47.863 0.000 -56.117 -51.701
PROX_MRT -47.214 1.613 -0.134 -29.267 0.000 -50.376 -44.052
PROX_PARK -10.254 1.471 -0.034 -6.972 0.000 -13.136 -7.371
PROX_GOOD_PRI_SCH -7.886 0.295 -0.135 -26.736 0.000 -8.464 -7.308
PROX_MALL -27.610 1.656 -0.081 -16.677 0.000 -30.856 -24.365
PROX_SUPERMARKET -23.728 3.843 -0.028 -6.174 0.000 -31.260 -16.195
NUM_KINDERGARTEN 3880.350 644.851 0.028 6.017 0.000 2616.401 5144.299
NUM_CHILDCARE -4945.079 322.008 -0.076 -15.357 0.000 -5576.235 -4313.924
NUM_BUS_STOP -1534.475 204.053 -0.034 -7.520 0.000 -1934.431 -1134.518
NUM_PRI_SCH -19005.239 426.663 -0.224 -44.544 0.000 -19841.526 -18168.951
------------------------------------------------------------------------------------------------------------We can see here that we have a R-squared value of our multiple linear regression is very low at only 0.57, which means that this model can only represent about 57% of the variance present in the data This indicates that this model is not well fitted to the data. Hopefully our other models will perform better.
GWR
Let us now try Geographically Weighted Regression, which is similar to our Multiple Linear Regression, but also takes into account the location of resale flat in question as an independent variable.
First, we will have to convert our data into an SP object.
train_data_sp <- as_Spatial(train_data)
test_data_sp <- as_Spatial(test_data)
train_data_spclass : SpatialPointsDataFrame
features : 23656
extent : 11519.79, 42645.18, 28217.39, 48741.06 (xmin, xmax, ymin, ymax)
crs : +proj=tmerc +lat_0=1.36666666666667 +lon_0=103.833333333333 +k=1 +x_0=28001.642 +y_0=38744.572 +ellps=WGS84 +towgs84=0,0,0,0,0,0,0 +units=m +no_defs
variables : 16
names : storey_range, floor_area_sqm, remaining_lease, resale_price, PROX_CBD, PROX_ELDERCARE, PROX_HAWKER_CENTRE, PROX_MRT, PROX_PARK, PROX_GOOD_PRI_SCH, PROX_MALL, PROX_SUPERMARKET, NUM_KINDERGARTEN, NUM_CHILDCARE, NUM_BUS_STOP, ...
min values : 1, 70, 44, 250000, 87458.4329578266, 0.0000198943787433087, 30.6031805185926, 21.7933772276802, 45.419944744772, 34.9059764152408, 0.00000000221189111471176, 0.00000616602451959176, 0, 0, 0, ...
max values : 17, 145, 97, 1370000, 118330.164171714, 3301.63731686804, 2867.63031236184, 2129.08590009577, 2411.71566715079, 9298.87658944395, 2321.60688849192, 1571.31703651196, 8, 20, 19, ... Next, we have to calculate the appropriate bandwidth for our model to use.
# bw_adaptive <- bw.gwr(resale_price ~ floor_area_sqm +
# storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN +
# NUM_CHILDCARE + NUM_BUS_STOP +
# NUM_PRI_SCH,
# data=train_data_sp,
# approach="CV",
# kernel="gaussian",
# adaptive=TRUE,
# longlat=FALSE)# write_rds(bw_adaptive, "data/model/bw_adaptive.rds")
bw_adaptive <- read_rds("data/model/bw_adaptive.rds")bw_adaptive[1] 121Now that those are done, we can proceed to calibrate our GWR model.
# gwr_adaptive <- gwr.basic(formula = resale_price ~
# floor_area_sqm + storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE +
# NUM_BUS_STOP + NUM_PRI_SCH,
# data=train_data_sp,
# bw=bw_adaptive,
# kernel = 'gaussian',
# adaptive=TRUE,
# longlat = FALSE)# write_rds(gwr_adaptive, "data/model/gwr_adaptive.rds")
gwr_adaptive <- read_rds("data/model/gwr_adaptive.rds")gwr_adaptive ***********************************************************************
* Package GWmodel *
***********************************************************************
Program starts at: 2023-03-17 15:07:56
Call:
gwr.basic(formula = resale_price ~ floor_area_sqm + storey_range +
remaining_lease + PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL + PROX_SUPERMARKET +
NUM_KINDERGARTEN + NUM_CHILDCARE + NUM_BUS_STOP + NUM_PRI_SCH,
data = train_data_sp, bw = bw_adaptive, kernel = "gaussian",
adaptive = TRUE, longlat = FALSE)
Dependent (y) variable: resale_price
Independent variables: floor_area_sqm storey_range remaining_lease PROX_CBD PROX_ELDERCARE PROX_HAWKER_CENTRE PROX_MRT PROX_PARK PROX_GOOD_PRI_SCH PROX_MALL PROX_SUPERMARKET NUM_KINDERGARTEN NUM_CHILDCARE NUM_BUS_STOP NUM_PRI_SCH
Number of data points: 23656
***********************************************************************
* Results of Global Regression *
***********************************************************************
Call:
lm(formula = formula, data = data)
Residuals:
Min 1Q Median 3Q Max
-446088 -52126 -4264 47958 475641
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 263417.95635 12436.32072 21.181 < 0.0000000000000002
floor_area_sqm 2693.33446 85.65820 31.443 < 0.0000000000000002
storey_range 21484.90803 276.47442 77.710 < 0.0000000000000002
remaining_lease 3402.54398 47.75189 71.255 < 0.0000000000000002
PROX_CBD -0.97112 0.07832 -12.400 < 0.0000000000000002
PROX_ELDERCARE -29.83367 0.97251 -30.677 < 0.0000000000000002
PROX_HAWKER_CENTRE -53.90901 1.12631 -47.863 < 0.0000000000000002
PROX_MRT -47.21443 1.61322 -29.267 < 0.0000000000000002
PROX_PARK -10.25360 1.47059 -6.972 0.0000000000031964
PROX_GOOD_PRI_SCH -7.88571 0.29494 -26.736 < 0.0000000000000002
PROX_MALL -27.61043 1.65562 -16.677 < 0.0000000000000002
PROX_SUPERMARKET -23.72765 3.84306 -6.174 0.0000000006760400
NUM_KINDERGARTEN 3880.35001 644.85053 6.017 0.0000000017980339
NUM_CHILDCARE -4945.07940 322.00765 -15.357 < 0.0000000000000002
NUM_BUS_STOP -1534.47450 204.05269 -7.520 0.0000000000000567
NUM_PRI_SCH -19005.23870 426.66327 -44.544 < 0.0000000000000002
(Intercept) ***
floor_area_sqm ***
storey_range ***
remaining_lease ***
PROX_CBD ***
PROX_ELDERCARE ***
PROX_HAWKER_CENTRE ***
PROX_MRT ***
PROX_PARK ***
PROX_GOOD_PRI_SCH ***
PROX_MALL ***
PROX_SUPERMARKET ***
NUM_KINDERGARTEN ***
NUM_CHILDCARE ***
NUM_BUS_STOP ***
NUM_PRI_SCH ***
---Significance stars
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 84970 on 23640 degrees of freedom
Multiple R-squared: 0.5698
Adjusted R-squared: 0.5695
F-statistic: 2088 on 15 and 23640 DF, p-value: < 0.00000000000000022
***Extra Diagnostic information
Residual sum of squares: 170665117245150
Sigma(hat): 84941.53
AIC: 604142.7
AICc: 604142.7
BIC: 580795.1
***********************************************************************
* Results of Geographically Weighted Regression *
***********************************************************************
*********************Model calibration information*********************
Kernel function: gaussian
Adaptive bandwidth: 121 (number of nearest neighbours)
Regression points: the same locations as observations are used.
Distance metric: Euclidean distance metric is used.
****************Summary of GWR coefficient estimates:******************
Min. 1st Qu. Median
Intercept -6154824945.5870 -5980688.7336 -564871.6203
floor_area_sqm -56518.3667 1736.7971 2672.7747
storey_range 6036.0824 9575.7295 11709.6092
remaining_lease -49743.7705 997.8640 3445.1829
PROX_CBD -3857.4104 -35.6151 5.3676
PROX_ELDERCARE -23948.4825 -37.6002 14.6073
PROX_HAWKER_CENTRE -10108.5821 -60.2183 -5.4912
PROX_MRT -2187.8964 -102.4279 -49.7678
PROX_PARK -14749.9001 -62.2603 -7.3206
PROX_GOOD_PRI_SCH -13928.7632 -54.5187 -5.4199
PROX_MALL -8076.9902 -63.1230 -13.0817
PROX_SUPERMARKET -3066.1555 -62.1938 -6.3848
NUM_KINDERGARTEN -125133.3949 -6882.7294 -1237.0524
NUM_CHILDCARE -39922.2288 -3555.5447 197.5141
NUM_BUS_STOP -23521.3718 -1500.0337 208.1895
NUM_PRI_SCH -1040510.3918 -5736.6423 421.0523
3rd Qu. Max.
Intercept 3791086.5663 385958657.38
floor_area_sqm 4590.8800 93004.54
storey_range 13887.7082 26827.90
remaining_lease 5948.7405 9941.57
PROX_CBD 63.6000 59412.59
PROX_ELDERCARE 64.9545 5647.81
PROX_HAWKER_CENTRE 42.4226 3989.74
PROX_MRT 5.9892 56003.29
PROX_PARK 33.5792 7434.86
PROX_GOOD_PRI_SCH 46.7582 3336.86
PROX_MALL 46.9820 13918.58
PROX_SUPERMARKET 34.0028 710.33
NUM_KINDERGARTEN 4781.0752 387092.01
NUM_CHILDCARE 2333.1064 24356.13
NUM_BUS_STOP 1797.7391 63833.78
NUM_PRI_SCH 6128.9843 2235361.28
************************Diagnostic information*************************
Number of data points: 23656
Effective number of parameters (2trace(S) - trace(S'S)): 1449.847
Effective degrees of freedom (n-2trace(S) + trace(S'S)): 22206.15
AICc (GWR book, Fotheringham, et al. 2002, p. 61, eq 2.33): 567053
AIC (GWR book, Fotheringham, et al. 2002,GWR p. 96, eq. 4.22): 565782.6
BIC (GWR book, Fotheringham, et al. 2002,GWR p. 61, eq. 2.34): 552562.7
Residual sum of squares: 32166641819946
R-square value: 0.91892
Adjusted R-square value: 0.913626
***********************************************************************
Program stops at: 2023-03-17 15:13:20 Once again, all our independent variable are noted to be statistically significant. With the additional of the geographic weights, we can see that our R-squared value drastically improves to 0.91892 in this model!
RF
Next, let us try random forest. However, for this method we will need to remove the geometry from our dataset first, so we will do that and store our coordinates into RDS for use later.
coords_train <- st_coordinates(train_data)
coords_test <- st_coordinates(test_data)train_data_nogeo <- train_data %>%
st_drop_geometry()
test_data_nogeo <- test_data %>%
st_drop_geometry()Since Random Forest has some degree of randomness to it, let us first set a seed.
set.seed(415)Now we can calibrate our random forest model.
# rf <- ranger(resale_price ~ floor_area_sqm + storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE +
# NUM_BUS_STOP + NUM_PRI_SCH,
# data=train_data_nogeo)# write_rds(rf, "data/model/rf.rds")
rf <- read_rds("data/model/rf.rds")print(rf)Ranger result
Call:
ranger(resale_price ~ floor_area_sqm + storey_range + remaining_lease + PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE + PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL + PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE + NUM_BUS_STOP + NUM_PRI_SCH, data = train_data_nogeo)
Type: Regression
Number of trees: 500
Sample size: 23656
Number of independent variables: 15
Mtry: 3
Target node size: 5
Variable importance mode: none
Splitrule: variance
OOB prediction error (MSE): 1182442905
R squared (OOB): 0.9294964 From our result, we can see we have an R-squared of 0.9294964! This is even better than our Geographically Weighted Regression, despite not having used our coordinate information at all!
GWRF
Lastly, we shall try Geographically Weighted Random Forest. Similar to how GWR was just our MLR with our data coordinates added to it, GWRF would be Random Forest, but with our coordinate data added back into our model as an independent variable.
Since we are working with spatial data, once again, we will need to calculate an optimal bandwidth for our model. Let us first look at our training dataset once again.
glimpse(train_data)Rows: 23,656
Columns: 17
$ storey_range <dbl> 2, 1, 1, 3, 3, 3, 3, 2, 4, 3, 5, 1, 3, 4, 2, 2, 1, …
$ floor_area_sqm <dbl> 92, 92, 91, 92, 92, 98, 92, 92, 92, 92, 92, 109, 97…
$ remaining_lease <dbl> 59, 57, 58, 57, 57, 56, 55, 56, 57, 57, 58, 58, 55,…
$ resale_price <dbl> 370000, 375000, 380000, 385000, 410000, 410000, 410…
$ geometry <POINT [m]> POINT (30770.07 39578.64), POINT (30292.01 38…
$ PROX_CBD <dbl> 99382.17, 99759.15, 100274.27, 99452.15, 99709.54, …
$ PROX_ELDERCARE <dbl> 1085.67795, 150.39052, 722.42472, 98.16285, 592.694…
$ PROX_HAWKER_CENTRE <dbl> 444.2515, 205.0009, 449.5734, 319.0679, 258.9414, 4…
$ PROX_MRT <dbl> 1048.6764, 757.4007, 456.7509, 886.8553, 553.7966, …
$ PROX_PARK <dbl> 752.0454, 648.4302, 367.7768, 390.6401, 495.0982, 2…
$ PROX_GOOD_PRI_SCH <dbl> 222.3635, 1343.6417, 826.9346, 1174.3821, 710.3726,…
$ PROX_MALL <dbl> 1216.2873, 844.4977, 560.0960, 930.4149, 719.5534, …
$ PROX_SUPERMARKET <dbl> 418.4204, 194.6009, 443.5109, 426.9715, 192.5617, 2…
$ NUM_KINDERGARTEN <dbl> 1, 0, 1, 1, 1, 1, 2, 1, 0, 0, 1, 1, 1, 1, 1, 1, 1, …
$ NUM_CHILDCARE <dbl> 2, 3, 3, 3, 3, 2, 6, 3, 3, 3, 3, 3, 5, 2, 3, 5, 3, …
$ NUM_BUS_STOP <dbl> 4, 7, 10, 4, 8, 2, 8, 7, 6, 7, 7, 7, 8, 8, 11, 5, 1…
$ NUM_PRI_SCH <dbl> 3, 3, 5, 4, 5, 3, 2, 5, 3, 4, 3, 2, 3, 5, 4, 2, 4, …Here we can see that we have about 23k data points. As it takes a long time for the algorithm to find the optimal bandwidth, let us use a small sample size. A sample size of 2.5k easily covers more than 10% of our dataset, and taking the first 2.5k rows of our dataset should correspond to a sample of the first 2 months or so of our training data (since the data was not reordered).
sample_train <- train_data[1:2500, ]
sample_trainSimple feature collection with 2500 features and 16 fields
Geometry type: POINT
Dimension: XY
Bounding box: xmin: 17706.54 ymin: 28287.8 xmax: 40610.11 ymax: 41295.7
Projected CRS: SVY21 / Singapore TM
# A tibble: 2,500 × 17
storey_ra…¹ floor…² remai…³ resal…⁴ geometry PROX_CBD PROX_ELDER…⁵
<dbl> <dbl> <dbl> <dbl> <POINT [m]> <dbl> <dbl>
1 2 92 59 370000 (30770.07 39578.64) 99382. 1086.
2 1 92 57 375000 (30292.01 38439.17) 99759. 150.
3 1 91 58 380000 (29872 39555.56) 100274. 722.
4 3 92 57 385000 (30613.6 38603.54) 99452. 98.2
5 3 92 57 410000 (30399.59 39119.25) 99710. 593.
6 3 98 56 410000 (28960.32 39342.78) 101163. 347.
7 3 92 55 410000 (29179.92 38822.08) 100899. 251.
8 2 92 56 418000 (30237.21 39012.48) 99862. 454.
9 4 92 57 420000 (30265.47 38397.28) 99782. 175.
10 3 92 57 420000 (30263.23 38499.84) 99793. 85.5
# … with 2,490 more rows, 10 more variables: PROX_HAWKER_CENTRE <dbl>,
# PROX_MRT <dbl>, PROX_PARK <dbl>, PROX_GOOD_PRI_SCH <dbl>, PROX_MALL <dbl>,
# PROX_SUPERMARKET <dbl>, NUM_KINDERGARTEN <dbl>, NUM_CHILDCARE <dbl>,
# NUM_BUS_STOP <dbl>, NUM_PRI_SCH <dbl>, and abbreviated variable names
# ¹storey_range, ²floor_area_sqm, ³remaining_lease, ⁴resale_price,
# ⁵PROX_ELDERCAREOnce again, we will seperate out our coordinates in order to put them separately into the model.
sample_train_coords <- st_coordinates(sample_train)
sample_train_nogeo <- sample_train %>% st_drop_geometry()And now we can calibrate our bandwidth.
# gwrf_adapative_bw <- grf.bw(formula = resale_price ~
# floor_area_sqm + storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE +
# NUM_BUS_STOP + NUM_PRI_SCH,
# sample_train_nogeo,
# kernel="adaptive",
# coords=sample_train_coords,
# step = 10,
# bw.min = 300)However, after running this function for 16 hours straight with Rstudio being the only app running on my computer, it was still unable to converge on an optimal bandwidth. So in order to move on, I will be using the bandwidth with the highest R squared from the logs, which happened to be:
Bandwidth: 620 with an R2 of Local Model: 0.928400292072046.
We can now calibrate our GWRF using this bandwidthm along with our prepared dataframe and coordinates from previously.
# gwRF_adaptive <- grf(formula = resale_price ~
# floor_area_sqm + storey_range + remaining_lease +
# PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE +
# PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL +
# PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE +
# NUM_BUS_STOP + NUM_PRI_SCH,
# dframe=train_data_nogeo,
# bw=620,
# kernel="adaptive",
# ntree = 20,
# coords=coords_train)# write_rds(gwRF_adaptive, "data/model/gwRF_adaptive.rds")
gwRF_adaptive <- read_rds("data/model/gwRF_adaptive.rds")gwRF_adaptive$Global.ModelRanger result
Call:
ranger(resale_price ~ floor_area_sqm + storey_range + remaining_lease + PROX_CBD + PROX_ELDERCARE + PROX_HAWKER_CENTRE + PROX_MRT + PROX_PARK + PROX_GOOD_PRI_SCH + PROX_MALL + PROX_SUPERMARKET + NUM_KINDERGARTEN + NUM_CHILDCARE + NUM_BUS_STOP + NUM_PRI_SCH, data = train_data_nogeo, num.trees = 20, mtry = 5, importance = "impurity", num.threads = NULL)
Type: Regression
Number of trees: 20
Sample size: 23656
Number of independent variables: 15
Mtry: 5
Target node size: 5
Variable importance mode: impurity
Splitrule: variance
OOB prediction error (MSE): 1296333810
R squared (OOB): 0.9227056 Our R-squared for this model is 0.9227056, which is slightly lower than our Random Forest model interestingly enough. However, it is still quite high, and we must see how it performs on our test data before drawing any conclusions on its effectiveness compared to other models.
Model Prediction
We can now move on to predicting on our test data to see the effectiveness of our models on data it has not seen before. In this section, we will be testing on MLR, RF, and GWRF. GWR will be excluded as it did not perform as well as our Random Forest methods, and takes a long time to run (as well as we ran into some errors when trying to call predict on the model).
MLR
Let us start by using the predict() function on our price_mlr model.
# mlr_pred <- predict(price_mlr, test_data)
# write_rds(mlr_pred, "data/model/mlr_pred.rds")
mlr_pred <- read_rds("data/model/mlr_pred.rds")mlr_pred_df <- as.data.frame(mlr_pred)
test_data_p_mlr <- cbind(test_data, mlr_pred_df)
rmse_mlr <- rmse(test_data_p_mlr$resale_price, test_data_p_mlr$mlr_pred)
rmse_mlr[1] 94109.72ggplot(data = test_data_p_mlr,
aes(x = mlr_pred,
y = resale_price)) +
geom_point() +
geom_abline(color="red")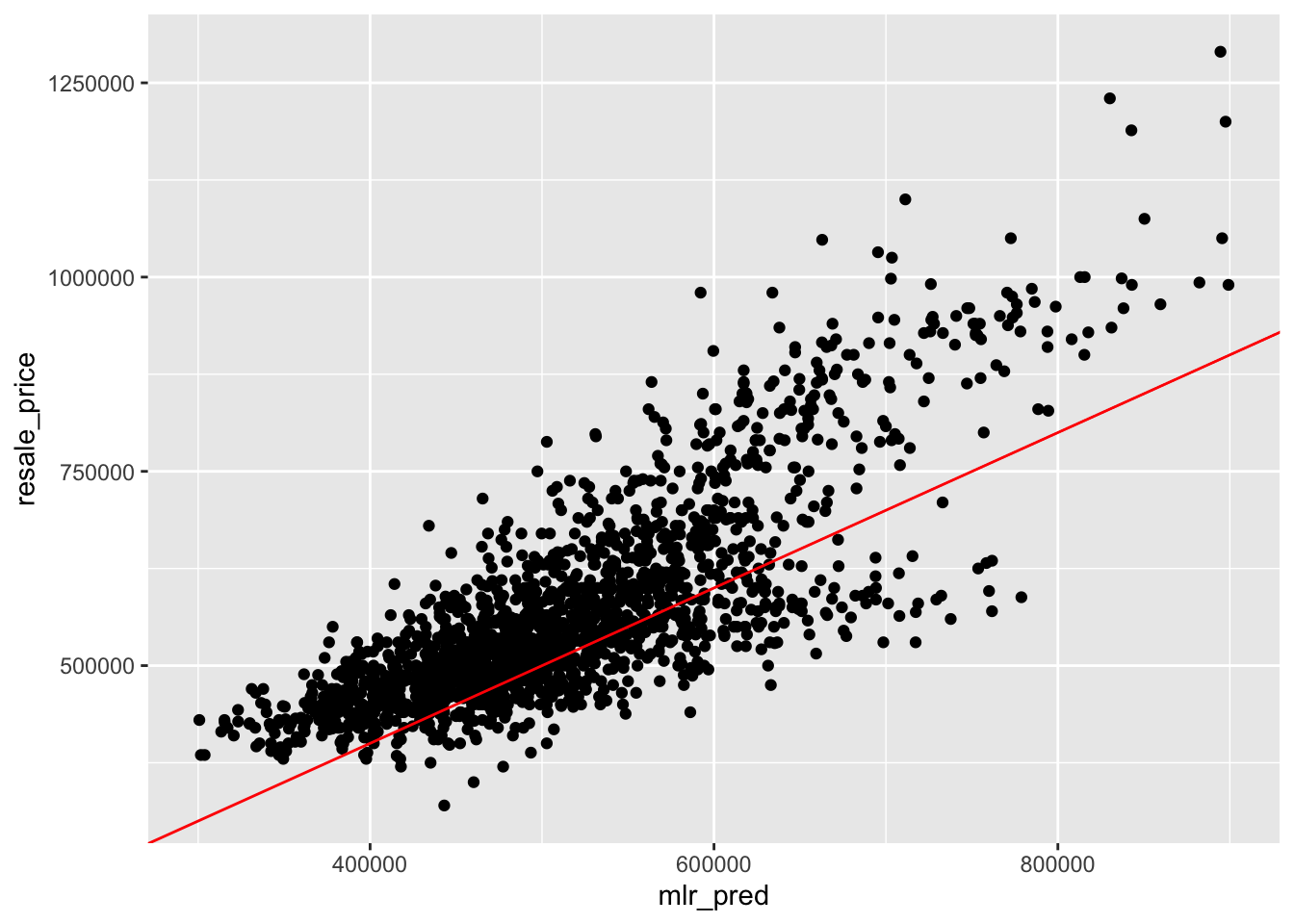
For this model, we can see our data is quite spread from the Line of Equality (where resale_price = mlr_pred), showing that our model does not fit our data well. A lot of our data points lie above the Line of Equality, suggesting that our model is under-predicting the price more than often.
RF
# rf_pred <- predict(rf, test_data_nogeo)
# write_rds(rf_pred, "data/model/rf_pred.rds")
rf_pred <- read_rds("data/model/rf_pred.rds")rf_pred_df <- as.data.frame(rf_pred)
test_data_p_rf <- cbind(test_data, rf_pred_df)
rmse_rf <- rmse(test_data_p_rf$resale_price, test_data_p_rf$prediction)
rmse_rf[1] 50043.6ggplot(data = test_data_p_rf,
aes(x = prediction,
y = resale_price)) +
geom_point() +
geom_abline(color="red")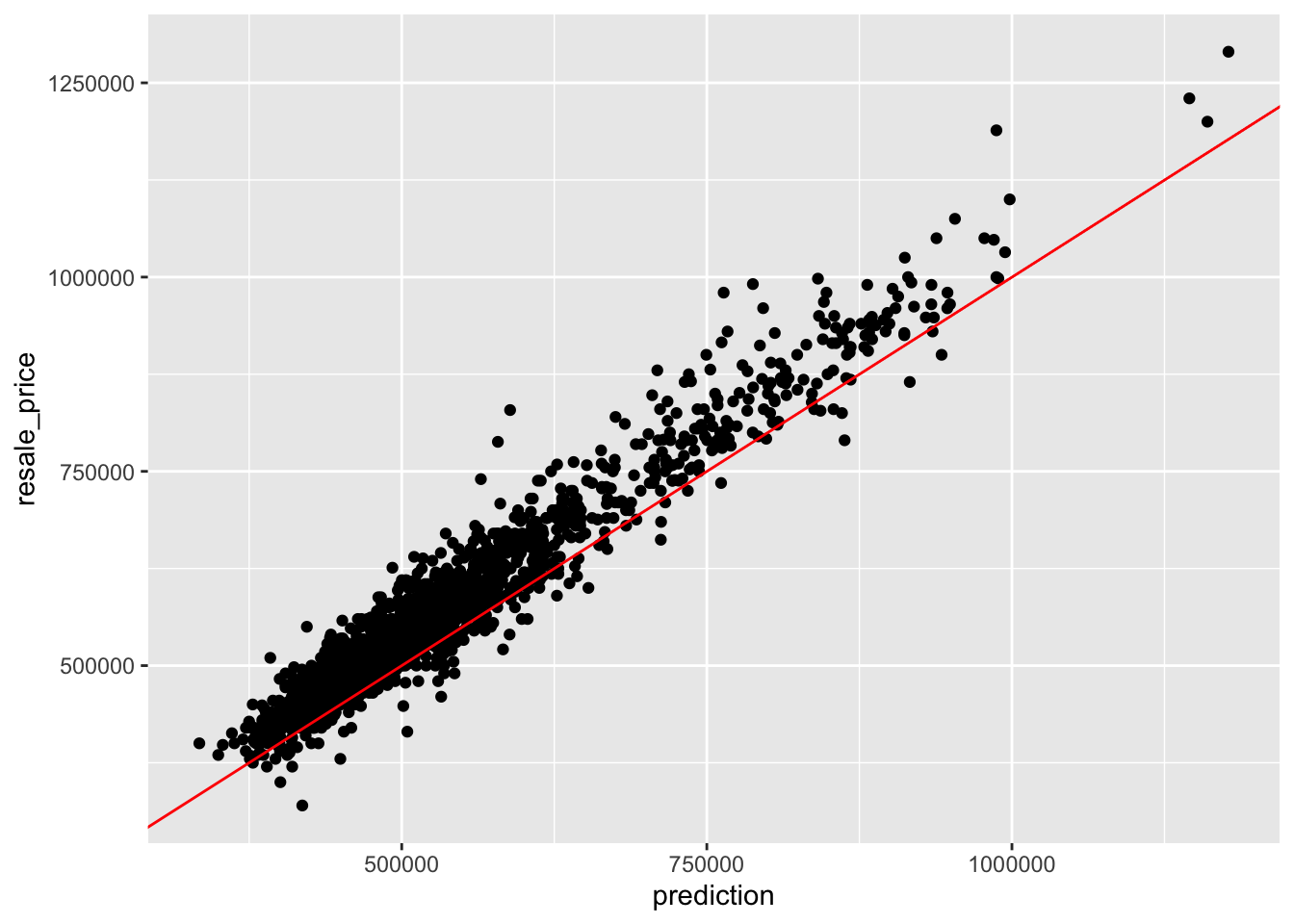
Here we can see that our data points are much closer to our Line of Equality, demonstrating that our random forest is much better than our MLR at accurately predicting the price of resale flats on our unseen data.
GWRF
test_data_with_coords <- cbind(test_data, coords_test) %>%
st_drop_geometry()
# gwRF_pred <- predict.grf(gwRF_adaptive,
# test_data_with_coords,
# x.var.name="X",
# y.var.name="Y",
# local.w=1,
# global.w=0)
# write_rds(gwRF_pred, "data/model/gwRF_pred.rds")
gwRF_pred <- read_rds("data/model/gwRF_pred.rds")gwRF_pred_df <- as.data.frame(gwRF_pred)
test_data_p <- cbind(test_data, gwRF_pred_df)
rmse_gwrf <- rmse(test_data_p$resale_price, test_data_p$gwRF_pred)
rmse_gwrf[1] 46042.97ggplot(data = test_data_p,
aes(x = gwRF_pred,
y = resale_price)) +
geom_point() +
geom_abline(color="red")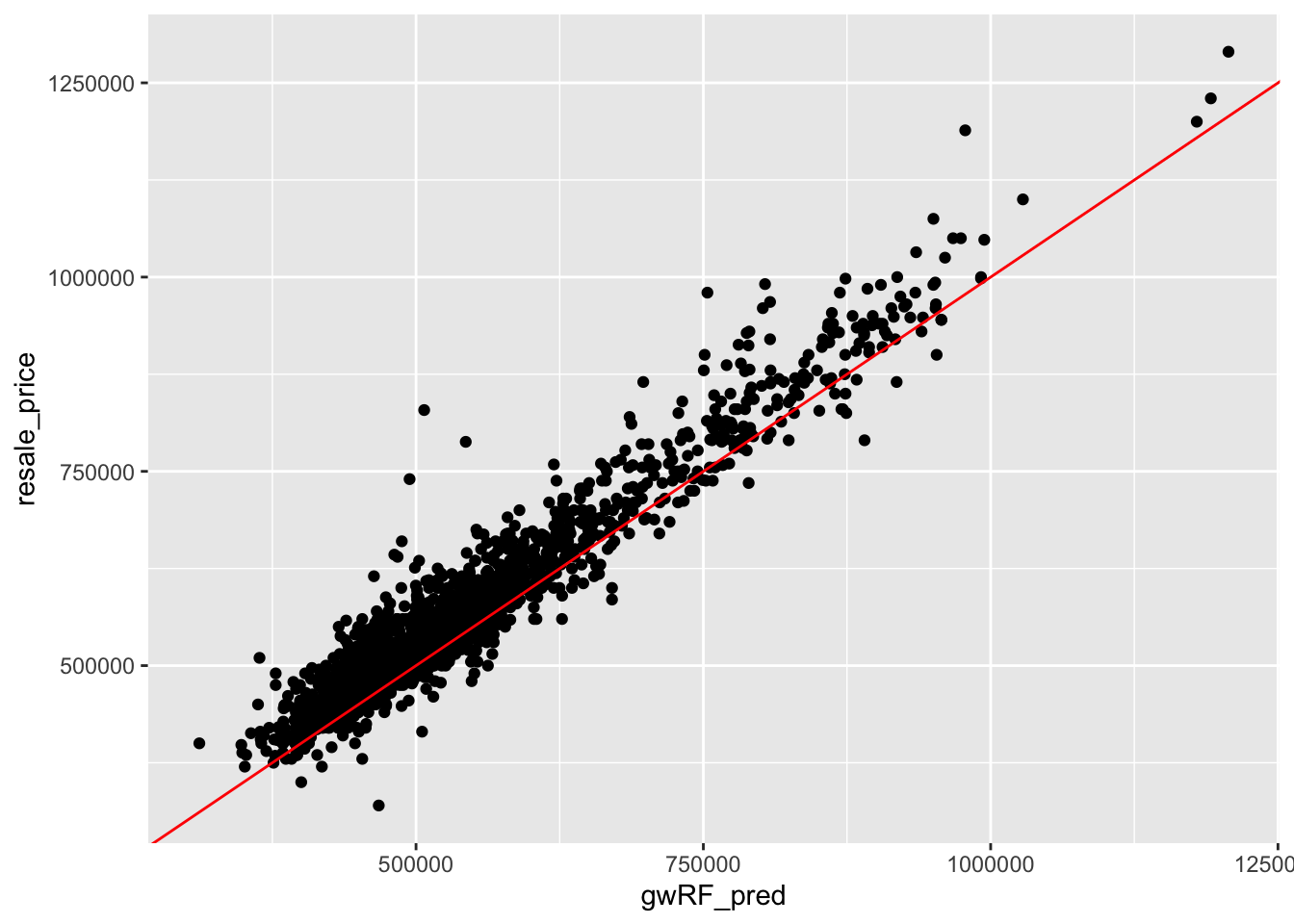
Once again, we can see that our predictions by our GWRF model line close to our Line of Equality, signifying good fit on our unseen test data set. Our results look quite similar to that of our Random Forest, so let us evaluate their goodness of it using RMSE in the next section.
Evaluation & Conclusion
Now that we have carried out our prediction on all 3 of our chosen models on our test data, we can now compare their effectiveness using RMSE. RMSE stands for Root Mean Square Error, which takes the root of the average squared (euclidean) distance between the actual resale price value and the predicted resale price value as a measure of how well the model fits / predicts the data. For this metric, the smaller the RMSE, the better the fit of the model as there is less average error in the model’s prediction.
rmse_mlr[1] 94109.72rmse_rf[1] 50043.6rmse_gwrf[1] 46042.97And from these RMSEs, we can determine that Geographically Weighted Random Forest is our clear winner here, having the lowest RMSE among the 3. Random Forest, although having a higher R-Squared value in training, does not perform better than our Geographically Weighted Random Forest model when generalised onto unseen testing data. And of course our OLS MLR model performs the worst, as expected after seeing even our training data having a poor performance and low R-squared value.
Unfortunately, unlike regression, we are unable to really examine and break down the factors that goes into splitting up our random forest and how they affect the trees. However, we can suggest improvements to this model. In this analysis, due to the limited time and computing power available, we limited this model to only 20 trees for each of the local random forests. This greatly limits the model’s ability to grow fine-grained divisions due to the limit number of trees. Therefore, this Geographically Weighted Random Forest model could be further improved by increasing the number of ntrees specified when training the model.
References
A big thank you to these senior’s works as provided by prof:
Take-Home Exercise 3: Hedonic Pricing Models for Resale Prices of Public Housing in Singapore by MEGAN SIM TZE YEN.
Take-home Exercise 3 by NOR AISYAH BINTE AJIT.
Without these two exemplary senior’s works, as well as prof’s In-Class exercises, I would not have been able to complete this assignment.